The necessity of Structural Conceptions

La matematica moderna sembra essere fondamentalmente strutturale. Sembra che abbiamo una particolare propensione a reificare, a rendere oggetti i concetti, come se volessimo riavvicinarli al mondo reale ....Perche?
Probabilmente ciò avviene perchè abbiamo la sensazione che non possiamo eseguire un processo finchè non c'è un oggetto su cui eseguirlo, e finchè non c'è un'altro oggetto prodotto dal processo sul primo oggetto.

Esperimento (parte 1):

Definizione: una Promenade è l'insieme di tutti i numeri naturali tra 1 e 25 con le seguenti funzioni:

$A(x)=x+5 per x \in P, x \le 20$
$B(x)=x-5 per x \in P, x > 5$
$C(x)=x+1 per x \in P, x mod 5 \ne 0$
$D(x)=x-1 per x \in P, x mod 5 \ne 1$

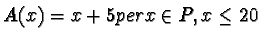
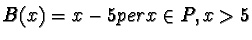
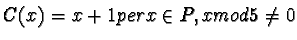
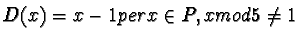
Ogni composizione delle suddette funzioni si dice stroll.
Diciamo che uno stroll s va da a a b se e solo se A(a)=b.

Esempio: lo stroll $S \circ D^3 \circ A^2$ va da 5 a 17:
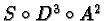$(A\circ D^3\circ A^2)(5)=(D^3\circ A^2)(10)=...=A(12)=17$

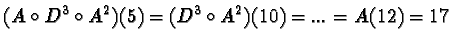
Compiti:

1) Trova un esempio di stroll che va da 11 a 3.
2) Trova tutti i numeri che possono essere raggiunti a partire da 9 senza usare D e D.
2) Senza guardare alle risposte che hai dato alla domanda 1), dai un esempio nuovo di stroll che va da 11 a 3.

Ora potete guardare 6 e provare a riaffrontare i compiti precedentemente affrontati. In questo caso il compito dovrebbe essere risultato nettamente più facile, grazie alla rappresentazione grafica che in qualche modo ha permesso di ``reificare'' gli oggetti nei nodi ed i processi nei trattini di collgamento, e gli stroll nei cammini sulla griglia.
Questo esempio lo portiamo per far vedere come in effetti, per lo meno in contesti di problem solving un'approccio strutturale può aiutare molto.

  

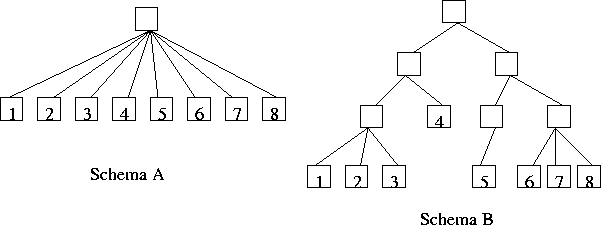
Figure 4: Ogni informazione può essere immagazzinata secondo differenti schemi. Ad esempio i due schemi in figura contengono le stesse informazioni (1,2,...,8). Lo schema A è sequenziale, poco profondo e largo. Come risultato di una reificazione (es. 1,2,3 diventano un oggetto etc.) può essere riorganizzato in una struttura più profonda e meno larga, come quella dello schema B. Con la nuova organizzazione tutti i processi cognitivi (immagazzinare ed estrarre informazioni) diventano molti più veloci.

Il motiv diciamo ``tecnico'', per cui Sfard sostiene che un approccio strutturale sia necessario, è senza gli oggetti astratti l'attivià mentale sembra essere molto più difficile. Dato che non siamo super computers abbiamo bisogno di organizzare le informazioni immagazzinate in modo che sia facile gestirle, ``processare'' una grossa serie di informazioni organizzate sequensialmente sarebbe praticamente impossibile (vedi 4). Per cui spezzettiamo la sequenza di informazioni in parti più piccole che formano delle unità , quelli che Sfarda chiama oggetti stratti (vedi 4). Queste entità cognitive compatte effettivamente prvengono un sovraccarico della memoria di lavoro.
Ad un certo punto della formazione della conoscenza, l'assenza di una concezione strutturale, può impedire ulteriori sviluppi. Come la quantità di informazioni cresce il vecchio schema (sequenziale) può saturarsi e divenire difficilmente arricchibile. Secondo Sfard non è un caso se il passaggio dall'algebra retorica a quella simbolica sia avvenuto nel XVI secolo, quando la materia era diventata troppo complessa; ed ancora non è un caso se in quel momento molti diversi sistemi di simboli sono stati inventati simultaneamente da matematici che lavoravano indipendentemente⁸.
Detto che da un punto di vista quasi ``fisioligico'' il pensiero strutturale aiuta a superare i limiti della nostra memoria di lavoro (secondo me della memoria in generale), Sfard sosotiene che ad un livello meno tecnico, più filosofico, si può dire che, in matematica, la transizione da processi ad oggetti astratti accresce il nostro ``senso di comprensione della matematica''. Dopo tutto, dice, la reificazione accresce le abilità di problem-solving e di apprendimento, per cui più il nostro approccio è strutturale e più ci sentiamo sicuri di quello che facciamo. Come esempio Sfard richiama l'esperimento proposto in questo articolo.
In conclusione Sfard sostiene che le concezioni strutturali sono ciò che osggiace la ``comprensione relazionale'' (en. ``relational understanding'') definita da Skemp (1976) come ``sapere sia cosa facciamo che perchè lo facciamo'', o in altre parole come ``avere sia le regole che le ragioni soggiacenti alle stesse''. Un approccio puramente operativo solitamente non garantisce più della comprensione strumentale⁹, indicato da Skemp come aver ``regole senza ragioni''<sup>10</sup>. A questi due tipi di approcci indicati da Skemp, Sfard ne aggiunge un altro che chiama ``ragioni senza regole'', riferendosi ad una specie di comprensione puramente intuitiva che si ottiene in quei casi un cui una vaga concezione strutturale si forma prima che si siano formate pienamente le basi operative¹¹. Questo è forse il tipo di comprensione che avevano i matematici all'inizio dello sviluppo del concetto di funzione¹². Secondo Sfard la storia mostra che tale tipo di comprensione può non essere sufficiente per creare una nuova teoria matematica vera e propria, me può essere molto d'aiuto nello scoprire teoremi e nel decidere le direzioni da seguire negli sviluppi futuri.