La doppia natura delle concezioni matematiche (o concetti matematici?)

Tanto per cominciare distinguiamo le parole ``concetto'' e ``concezione''; indichiamo cosa intendiamo con questi due termini:

• concetto: (a volte diremo ``nozione'') con questo termine ci riferiamo ad un ``blocco'' di conoscenza matematica (lei parla di ``building block of mathematics'') inserito in un contesto teorico matematico. In altre parole un concetto è un pezzo di matematica visto all'interno della Matematica (notare le M maiuscola)
• concezione: con ``concezione'' intendiamo un insieme di rappresentazioni interne evocate da un concetto; in altre parole la concezione è la controparte soggettiva del concetto, ``interna'' al mondo della conoscenza del singolo individuo

Dal punto di vista del linguaggio la matematica per certi versi sembra essere del tutto analoga alle altre scienze. In effetti, come biologi o fisici o altri, il matematico, solitamente parla di certi ``universi'' popolati da certi ``oggetti''. I vari oggetti hanno delle caratteristiche proprie e sono governati da leggi ben definite. Il matematico descrive le proprietà di insiemi e numeri in maniera analoga a come lo scenziato descrive la struttura di molecole e cristalli. Frasi del tipo ``esiste una funzione tale che ...'', in matematica (moderna), sono altrettanto comuni come affermazioni sull'esistenza di certe molecole subatomiche in fisica.
Diversamente dagli oggetti materiali, però , i costrutti della matematica avanzata<sup>1</sup> sono totalmente inaccessibili ai nostri sensi, essi possono essere visti solo dagli occhi della mente. Quando disegnamo (noi matematici) il grafico di una funzione, sappiamo bene che il segno sulla carta non è altro che una delle tante possibili rappresentazioni di un'entità astratta, che di suo non può né vista né toccata. Normalmente il matematico ragiona sull'esistenza e sulle proprietà di certe entità astratte senza preoccuparsi troppo di questioni ontologiche riguardanti l'esistenza ``reale'' delle entità in questione. Per un approfondimento sulla questione ontologica (cui forse accenneremo) potete guardare [15].
La capacità di vedere, in qualche modo, tali ``oggetti invisibili'' sembra essere una componente essenziale del sapersi muovere nella matematica. La mancanza di questa capacità può essere una delle principali ragioni per cui la matematica sembra essere praticamente impermeabile a molti soggetti (lei parla di ``well-formed minds'').

D'ora in avanti utilizzeremo la parola strutturale per indicare un approccio in cui le nozioni matematiche sono trattate come se esse corrispondessere in qualche modo ad oggetti astratti; questo non è l'unico approccio possibile, esiste anche quello operativo. Ad esempio una funzione può essere considerata come un processo di calcolo, la simmetria può essere interpretata come trasformazione; in entrambe questi due casi si può parlare di concezione operativa di una nozione matematica.
Vedere un'entità matematica come un oggetto significa essere in grado di riferirsi ad essa come se fosse una cosa reale, una struttura statica esistente da qualche parte nello spazio-tempo. Significa essere in grado di riconoscere l'idea nel suo insieme ed essere in grado di manipolarla come un tutt'uno, senza necessariamente occuparsi dei suoi dettagli. Hadamard [6] dice che pensare in maniera strutturale associa ad un concetto una fisiognomica che permette di pensare ad ``esso come una cosa unica, anche se complicata, nello stesso modo in cui vediamo la faccia di un uomo'' che in effetti è caratterizzata da molti particolari che per noi formano un tutt'uno.
In contrasto, interpretare una nozione come processo (approccio operativo) implica interpretarlo come un'entità ``potenziale'' (piuttosto che come un'entità vera), la quale esiste nel momento in cui viene utilizzata in una sequenza di azioni.
Pertanto, mentre la concezione strutturale è statica, instantanea, unificante, quella operativa è dinamica, seuenziale e dettagliata.
Sfard non sembra voler fare un trattato sulla distinsione tra i due approcci, si limita ad indicarli e descriverli brevemente, ma afferma che alla base della distinzione tra i due sta una profonda distinzione ontologica. Credo (non mi è ben chiaro), che si riferisca al fatto che un approccio operativo, che chi vede un'entità matematica come un processo che agisce su certi ogetti abbia bisogno di vedere certi oggetti come reali, come se la matematica offrisse processi per agire sul mondo reale.
Molto spesso i concetti matematici possono essere definiti o presentati sia in maniera operativa che strutturale, sono riportati alcuni esempi in 2 (Tabella 1).

 

Table 1: Descrizioni strutturali ed operative di alcune nozioni matematiche

Concetto	Definizione Strutturale	Definizione Operativa
Funzione	Insieme di coppie ordinate	Processo computazionale o metodo ben definito per passare da un sistema ad un altro
Simmetria	Proprietà di una generica forma	Trasformazione di una forma geometrica
Numero Naturale	Proprietà di una insieme o la classe di tutti gli insiemi finiti di eguale cardinalità	0 o ogni numero ottenuto da un altro naturale aggiungendo uno
Numero Razionale	Coppia di interi (considerata un'opportuna relazione d'equivalenza)	risultato della divisione tra interi
Cerchio	Il luogo dei punti equidistanti da un punto dato	una curva ottenuta ruotando un compasso intorno ad un punto dato

 

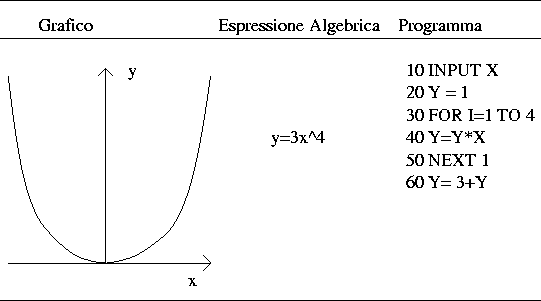
La doppia natura dei concetti matematici si può notare non solo nelle descrizioni verbali, ma anche analizzando vari modi di rappresentare simbolicamente i concetti in questione. Anche se una proprietà come la strutturalità di una concezione è interna al soggetto, piuttosto che nei simboli, è anche vero che alcuni tipi di rappresentazioni sono più suscettibili ad una interpretazione strutturale di altri. Ad esempio differenti modi di interpretare una funzione possono essere identificati nei tre diversi modi di rappresentare la funzione y=3x⁴ riportati in 1

  

Figure 1: Differenti rappresentazioni di una funzione

Il programma (in BASIC credo!) sembra corrispondere alla concezione operativa di funzione, in quanto la presenta come un processo computazionale, non come un'unica entita. Dall'altro lato abbiamo la rappresentazione grafica che combina le infinite coppie di punti della funzione in un'unica linea continua liscia, in questo modo queste infinite componenti della funzione possono essere ``prese'' (en. ``grasped'') come un tutt'uno (en. ``integrated whole''); il grafico, quindi, incoraggia l'approccio strutturale.
L'espressione algebrica può essere facilmente interpretata in entrambe i modi: può essere spiegata operativamente come una descrizione sintetica di certi calcoli, oppure strutturalmente come una relazione statica tra due grandezze. Questa particolare dualità di interpretazione corrisponde al già vastamente discusso doppio significato sel dimbolo di uguaglianza: ``='' può essere interpretato come simbolo di identità , oppure come un ``comando'' per eseguire delle operazioni ([1], [9], [10]).
La tipologia di una concezione si manifesta anche attraverso le speciali rappresentazioni interne al soggetto. Secondo quanto ormai noto ([12], [4], [2], [5]), i concetti matematici a volte sono visualizzati tramite ``immagini mentali'', mentre altre volte gli stessi concetti sono trattati soprattutto tramite rappresentazioni verbali.
Le immagini mentali, essendo compatte ed unificanti, sembrano supportare concezioni strutturali; le osservazioni introspettive di Hadamrd sembrano rinforszare questa supposizione: ``I need [an image] in order to have a simultaneous view of all elements ... to hold them toghether, to make a whole of them ...; to achieve synthesis ... and give the concept its physiognomy'' ([6], p.77). La visualizzazione, quindi, rende le idee astratte più tangibili ed incoraggia a trattarle quasi come se fossero entità materiali. In effetti le immagini mentali possono essere manipolate quasi come gli oggetti reali. La rappresentazione visiva è olistica (autoevidente?) per sua natura, e vari aspetti del concetto matematico posso essere estratti da essa tramite ``accesso casuale'' (en. ``random access''), senza un ordine di accesso prestabilito.
Di contro una rappresentazione verbale non può essere presa nel suo insieme come un tutt'uno (en. ``grasped at one glance''), ma deve invece essere processata sequenzialmente, quindi sembra essere più appropriata per rappresentare procedure di calcolo (o procedure in generale, direi). Per cui le rappresentazioni non visive sembrano essere più pertinenti al modo operativo di pensare.
A questo punto sfard chiarisce che non sta dicendo che c'è una corrispondenza biunivoca ta tipi di visualizzazione e tipi di concezione, suggerisce solo che alcuni tipi di rappresentazioni interne sembrano più vicine all'approccio strutturale ed altre a quello operativo.

A questo punto Sfard presenta una carrellata bibliografica per mostrare come questa doppia natura dei concetti matematici sia in realtà , seppur con nomi diversi e con diversi livelli di descrizione, già stata osservata e studiata da molti. In particolare possiamo elencare le seguenti ``dicotomie'' (vedi le citazioni di Sfard in [13] per i riferimenti bibliografici):

Astratto $\leftrightarrow$ Algoritmico (Halmos, 1985)
• Dichiarativo $\leftrightarrow$ Procedurale (Anderson, 1976)
• Dialettico $\leftrightarrow$ Algoritmico (Henrici, 1974)
• Figurale $\leftrightarrow$ Operativo (Piaget, 1970)
• Concettuale $\leftrightarrow$ Procedurale (Lesh, Landau 1983; Hiebert, 1985)
• Relazionale $\leftrightarrow$ Strumentale (Skemp, 1976)

Secondo Sfard anche le descrizioni date da tutti questi autori sono pocho chiare, uno degli scopi di questo articolo è chiarire la distinzione tra operativo e strutturale. Questa dicotomia (quella introdotta da Sfard) è simile alle altre, ma si distingue da loro per un paio di aspetti fondamentali:

• La maggior parte di coloro che hanno proposto le suddette dicotomie raramente hanno posto l'attenzione sulla questione delle assunzioni filosofiche, tacite, sottostanti ogni attività matematica; piuttosto si sono riferiti ad altri aspetti della matematica (come la sua struttura o il ruolo delle sue diverse componenti nel problem-solving), oppure si sono riferiti ai processi cognitivi coinvolti nella gestione delle conoscenze. Nella classificazione di Sfard, invece, si cerca di focalizzare contemporaneamente gli aspetti ontologici e quelli psicologici; in sostanza ci si focalizza sulla natura delle entità matematiche rispetto a come sono percepite da un soggetto.
• Mentre altre distinzioni portano ad una decomposizione della conoscenza matematica in due componenti separate (es. concetti vs. procedure), l'approccio di sfard, in quanto basato sulla complementarietà dei due ``poli'', tende a risaltare l'unità della conoscenza matematica.

Hiebert e Lefevre ([7], 1986) osservano: ``Storicamente i due tipi di conoscenza sono stati visti come entità separate, ... coesistenti come due vicini divisi ... In contrasto, c'è un crescente interesse, oggi, per come concetti e procedure sono collegati''. Ciononostante questo nuovo approccio non è ancora unificante: ``le discussioni correnti trattano le due forme di conoscenza come distinte''. Addirittura pare che si siano addirittura creati degli schieramenti pro-astratto e pro-procedurale; in generale l'astratto sembra essere molto più stimato del procedurale. Anche se tutti ammettono che la matematica ``algoritmica'' sia importante, l'opinione genrale che prevale è che questa sia matematica di serie B.
Sfard Invece rimarca il fatto che per lei le due forme di conoscenze (o concezioni, o approcci etc), anche se diverse, sono due facce della stessa medaglia. Di conseguenza bisogna parlare di dualità piuttosto che di dicotomia. Questo tipo di approccio priva di ogni significato la discussione su quale tipo di matematica sia migliore.
Insomma i due modi di interpretare la matematica sembrano essere entrambi necessari. Sfard cerca di mostrare che una profonda conoscenza che permette la creazione matematica può essere difficilmente raggiunta senza l'abilità di ``vedere'' gli oggetti astratti, ma d'altra parte una concezione strutturale è molto difficile da ottenere (questo, dice, forse è il motivo per cui molti sentono che l'abilità di sviluppare concezioni strutturali è ciò che distingue i matematici dai ``mortali''). Di contro Sfard cerca anche di mostrare che una profonda ``conoscenza'' (en. ``insight'') dei processi sottostanti i concetti matematici, e forse anche una certa abilità nello svolgere tali procedure (riferito a ``processi''), dovrebbe per lo meno in certi casi, essere visto come una base per la comprensione di tali concetti, piuttosto che come obiettivo finale. Insomma, una cosa del tipo capire e saper eseguire procedure come base per capire concetti, invece che saper eseguire procedure come scopo finale.
A questo punto viene posta una domanda tratta da [11]:

Come mai così tanti insegnanti, intelligenti, preparati e motivati, mettono così tanto interesse nel far sviluppare agli alunni particolari abilità nello svolgere le procedure dell'algebra e dell'aritmetica, nonstante decenni di avvertimenti di fare il contrario da parte dei cosiddetti ``esperti''? Cos'è che gli insegnanti sanno e gli altri no?