La formazione del concetto di numero

Per molto tempo la parola ``numero'' si è riferita a quelli che oggi chiamiamo ``numeri naturali''. Questo tipo di numeri ha origine nel processo del contare, lo si può vedere anche nei bambini che imparano a contare (vedi per esempio Piaget 1952): durante tale apprendimento, c'è uno stadio in il bambino è in grado di costruire una corrispondenza biunivoca tra le parole ``uno'', ``due'', ``tre'', ... e gli oggetti di un insieme dato, ma non usano l'ultima a parola ``contata'' per rispondere alla domanda ``quanti oggetti ci sono?''. Piuttosto in quel caso il bambino, per rispondere alla domanda, ripete il processo di contare. Questo fenomeno mostra chiaramente le origni operative del concetto di numero naturale: per il bambino quando si usa la parola ``numero'' ci si al processo del contare, non al suo prodotto astratto (il ``numero'').
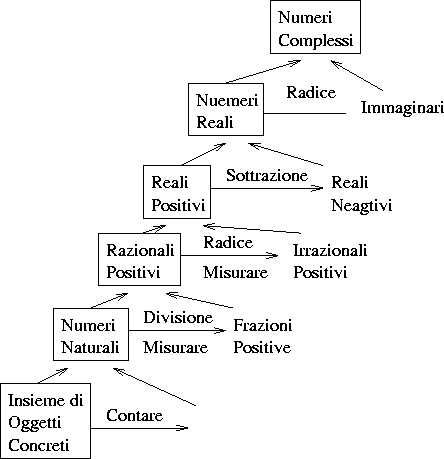
Il significato di numero si è evoluto molte volte nella storia, in 2 è schematizzato tutto il processo storico di formazione dei vari concetti di numero.

  

Figure 2: Lo sviluppo storico dei vari concetti di numero: per lunghi periodi i matematici hanno effettuato particolari manipolazioni su tipi di numeri ben conosciuti, prima di essere in grado di estrarre un oggetto astratto da tali processi, e di accettare le risultanti entità come nuovi tipi di oggetti matematicia

Il ``ratio'' tra due numeri interi inizialmente era trattato come una breve descrizione di un processo di misurazione (data l'unità di misura ...), piuttosto che come un numero. D'altra parte, alcune tracce di approcci puramente operativi al numero razionale sono stati osservati (Carpenter et al. 1980) anche negli studenti tredicenni di oggi, il 50% dei quali (in un campione, suppongo) non sono stati in grado di rappresentare un problema di divisione del tipo ``7 diviso 4'' sottoforma di frazione. In questi studenti la divisione tra interi era ancora solo un processo, che non poteva ancora essere visto come un'entità statica, la frazione.
In questa sede non stiamo a descrivere tutti i passaggi storici della formazione dei vari concetti di numeri. sfard propone il seguente schema che spiega i passaggi di 2 cone le tre seguenti fasi che si susseguono ad ogni passaggio:

1.

Fase preconettuale: i matematici prendono confidenza con certe operazioni su numeri già conosciuti (come nel caso di contare gli oggetti concreti; a questo punto, le manipolazioni di routine sono trattate per quello che sono: dei processi e niente più (non c'è bisogno di nuovi oggetti, dato che tutti i calcoli sono ancora ristretti a quelle procedure che producono numeri di tipo già noto).

2.

Fase di approccio predominantemente operativo: un nuovo tipo di numeri inizia ad emergere dai processi comunemente usati (cosa innesca questa reazione è l'uso di certe operazioni che prima erano viste come non permesse ma che ad un certo punto diventano accettate ed utili, anche se strane). A questo stadio, il nome, appena introdotto, per il nuovo numero, è più che altro un simbolo per indicare certe operazioni, e non si riferisce ad un vero oggetto. L'idea di un nuovo costrutto astratto, anche se già molto usato, continua ad evocare forti obiezioni a discussioni filosofiche accalorate.

3.

Fase strutturale: il numero in questione è riconosciuto come un vero e proprio oggetto matematico a tutti gli effetti. Da questo momento in poi, differenti processi saranno effettuati sui nuovi numeri, innescando nuovamente il ciclo, dando quindi la nascita a tipi di numeri più avanzati.

Riassumendo la storia dei numeri si presenta come una lunga catena di transizioni da concezioni operative a strutturali: passo dopo passo, processi effettuati su oggetti astratti già noti si sono convertiti in nuove entità compatte, si sono reificati, per diventare un nuovo tipo di costrutto statico indipendente.

La congettura di Sfard è che questo modello possa essere generalizzato allo sviluppo di molte altre idee matematiche.