Il ruolo delle concezioni operative e strutturali nella formazione dei concetti matematici: punto di vista psicologico

Cosa appare eveidente dagli esempi storici è che il processo di formazione di concezioni strutturali è molto lungo e spesso difficile e doloroso. Ma da dove vengno tali difficoltà ? Sfard cerca di rispondere da un punto di vista psicologico, limitandosi però al problema preliminare: ``il modello utilizzato per descrivere l'evoluzione storica dei concetti, può essere utilizzato per descrivere la formazione dei concetti in un individuo?''.
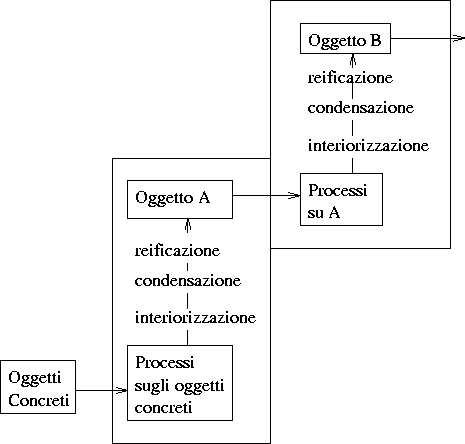
Le tre fasi descritte nell'esempio storico in questo caso prendono, rispettivamente i seguenti nomi: interiorizzazione, condensazione e reificazione.
Nella fase di interiorizzazione il soggetto prende confidenza con i processi che alla fine danno vita ad un nuovo concetto (come contare porta ai numeri naturali, sottrarre ai negativi, o manipolazioni algebriche portano al concetto di funzione). Questi processi sono operazioni effettuate agendo su oggetti matematici di livello più basso. Gradualmente il soggetto diventa abile ad eseguire tali processi. Il termine ``interiorizzazione'' Sfard lo usa nello stesso senso di Piaget: un processo è interiorizzato se ``può essere portato avanti mentalmente'', e per essere analizzato e confrontato necessita più di essere effettivamente eseguito.
Nel caso dei numeri negativi, questa corrisponde alla fase in cui la persona è abile a sottrarre numeri. Nel caso dei numeri complessi è quando il soggetto è particolarmente bravo ad utilizzare le radici quadrate. Nel caso delle funzioni, è quando l'idea di variabile è appresa e l'abilità di usare una formula per cercare i valori dipendenti da una variabile è acuisita.
La fase della condensazione è uno stadio in qui delle lunghe procedure vengono ristrette ad unità più maneggevoli. A questo livello la persona diventa sempre più capace di pensare ad un processo come una cosa unica, sensa sentire la necessità di entrare in dettaglio (e magari di eseguire il processo). È come tradurre una parte ricorrente di un programma al computer in una procedura autonoma: da questo momento in poi il soggetto si riferirà al processo in termini di relazioni input/otput piuttosto che indicando ogni singola operazione del processo. Come nel caso del computer, si può dare un nome a questà unità condensata. Questo è il momento in cui un nuovo concetto nasce ``ufficialmente''. Ogni difficoltà relativa all'output ottenuto può servire (vedi il caso della sottrazione prima di conoscere i negativi) come scintilla per far nascere l'idea di una nuova entità matematica.
Grazie alla condensazione diventa più facile combinare processi, confrontarli e generalizzarli. Un progesso nella condensazione si può manifestare anche tramite una crescente facilità di alternare le differenti rappresentazioni di un concetto.

...

Nel caso delle funzioni la condensazione si può manifestare con la capacità di gestire una funzione senza necessariamente guardare i suoi valori specifici. Infine, il soggetto, può studiare funzioni, disegnare i loro grafici, comperre diverse funzioni, o anche trovare le funzioni inverse².
La fase di condensazione dura finchè la nuova entità resta strettamante legata al processo che le ha dato origine. Solo quando una persona è in grado di concepire la nozione come un oggetto a se stante ed indipendente, possiamo dire che il concetto è stato rificato.
La reificazione si definisce quindi come uno ``spostamento ontologico'', un'abilità improvvisa di vedere qualcosa di familiare sotto una luce totalmente nuova (vedi esempio della lezione di Boero).
Mentre interiorizzazione e condensazione sono cambiamenti quantitativi e graudali, piuttosto che qualitativi, la reificazione è un salto quaitativo instantaneo: un processo si solidifica in un oggetto, in una struttura statica. Le varie rappresentazioni del concetto diventano semanticamente unificate da questo costrutto astratto, puramente immaginario. La nuova entità si stacca dal processo che l'ha generata e comincia a disegnare il proprio significato dal fatto di essere membro di una certa categoria (es. frazione diventa numero razionale). Ad un certo punto, questa categoria, piuttosto che un tipo di socrtuzione concreta, diventa la base ultima per proposizioni sulle'esistenza del nuovo oggetto<sup>3</sup>. Una persona può investigare le proprietà generali di tale categoria e le varie relazioni tra i suoi rappresentanti. Il soggetto può risolvere problemi che coinvolgono la ricerca di tutte le istanze della categoria che soddisfano certe condizioni date. Possono essere effettuati processi che coinvolgono la nuova entitaà come input (vedi i ``duali''). Nuovi oggetti matematici possono ora essere prodotti da quelli appena nati.
La reificazione è il punto in cui inizia l'interiorizzazione di concetti di livello più alto, quelli originati dai processi sulle entità appena reificate.

...

Nel caso delle funzioni la reificazione può essere messa in evidenza dall'abilità nel risolvere equazioni in cui le incognite sono funzioni (equazioni con parametri, o equazioni differenziali e funzionali), dall'abilità di parlare discutere le proprietà generali di diversi processi effettuati sulle funzioni (composizione, inversione), e dal riconoscere che la ``calcolabilità '' non è una caratteristica necessaria di un insieme di coppie ordinate per essere considerato una funzione.

  

Figure 3: Modello generale della formazione di un concetto

Come questo schema di sviluppo nei concetti possa essere influensato dall'insegnante è una grossa questione che la Sfard dice di non affrontare in questo articolo, qualcosa si può trovare in [15]. Qui si limita ad osservare che certe rappresentazioni, come nomi, simboli, grafici, possono avere un ruolo molto importante nel favorire condensazione e reificazione⁴. Come esempio storico riporta il piano di Argand, la cui invenzione e` stato il passo decisivo per far diventare i numeri complessi dei legittimi oggetti matematici. Per cui si presume che anche nell'apprendimento individuale tali rappresentazioni possano giocare un ruolo importante.
A questo punto dovrebbe essere chiaro che lo schema proposto da Sfard è una gerarchia, per cui ogni stadio non può essere raggiunto prima che i precedenti siano raggiunti o superati⁵. Bisogna comunque stare attenti agli ``stadi deviati'' come ad esempio la tendenza ad identificare una nozione con una sua rappresentazione.
Inoltre, l'ordine offerto dallo schema non è necessariamente rigido⁶ rigido, in effetti possiamo prendere noi stessi come esempi, in molti corsi universitari abbiamo saltato del tutto la fase operativa.