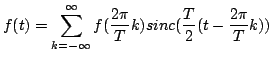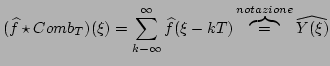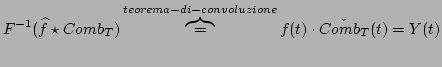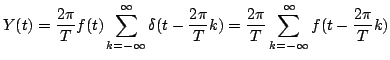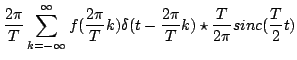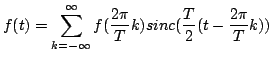Next: Ricostruzione
Up: Elaborazione Immagini: campionamento, aliasing
Previous: Aliasing
Teorema di campionamento Shannon. Sia
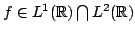 t.c. esiste
t.c. esiste 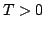 t.c.
t.c.
![$ supp\widehat{f}\subseteq[-\frac{T}{2},\frac{T}{2}]$](img66.png) . Allora
. Allora
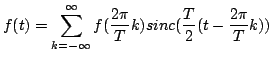 |
(4.1) |
dove
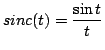 |
(4.2) |
Dimostrazione:
Facciamo il prolungamento periodico di
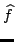 convolvendola con
convolvendola con 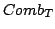 otteniamo
Che è una distribuzione temperata, per cui può essere vista
come trasformata di Fourier di (con
otteniamo
Che è una distribuzione temperata, per cui può essere vista
come trasformata di Fourier di (con 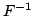 indico l'inversa
della trasformata)
E per le proprietà (2.10) di
indico l'inversa
della trasformata)
E per le proprietà (2.10) di 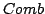 otteniamo
e per la definizione di
otteniamo
e per la definizione di 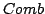 Questa funzione
Questa funzione 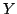 è quella che è responsabile
dell'aliasing. Se torniamo alla trasformata della funzione
campionata, ora che le ipotesi sul supporto di
è quella che è responsabile
dell'aliasing. Se torniamo alla trasformata della funzione
campionata, ora che le ipotesi sul supporto di
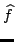 ci
garantiscono che nella sua periodizzazione non ci sono
sovrapposizioni, possiamo moltiplicare tale periodizzazione
ci
garantiscono che nella sua periodizzazione non ci sono
sovrapposizioni, possiamo moltiplicare tale periodizzazione
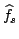 per una la funzione caratteristica
per una la funzione caratteristica
![$ \aleph_{[-\frac{T}{2},\frac{T}{2}]}$](img76.png) in modo da ottenere
per cui, per il teorema (2.13) di convoluzione
sviluppando il prodotto ci convoluzione si ottiene la tesi
in modo da ottenere
per cui, per il teorema (2.13) di convoluzione
sviluppando il prodotto ci convoluzione si ottiene la tesi



Next: Ricostruzione
Up: Elaborazione Immagini: campionamento, aliasing
Previous: Aliasing
Michele Cerulli
2000-10-29