


Next: Pulizia rumore
Up: Elaborazione Immagini: campionamento, aliasing
Previous: Teorema di campionamento shannon
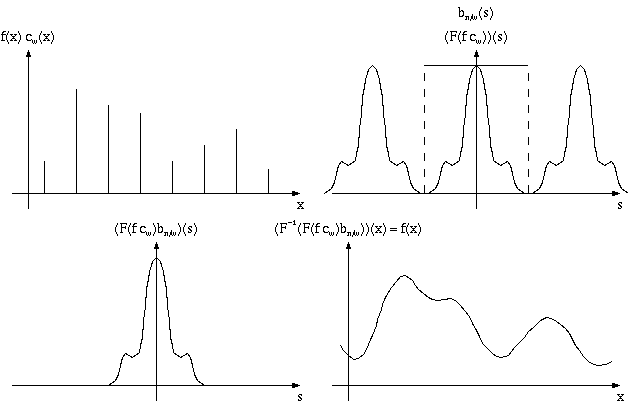 Il teorema di shannon ci dice come possiamo ricostruire la
funzione
Il teorema di shannon ci dice come possiamo ricostruire la
funzione 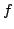 a partire dal campionamento
a partire dal campionamento 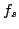 , a patto che
l'ampiezza degli intervalli di campionamento sia minore della
frequenza
, a patto che
l'ampiezza degli intervalli di campionamento sia minore della
frequenza 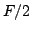 dell'enunciato, che è anche detta frequenza di
Nyquist. Quindi, da un punto di vista teorico, se il campionamento
è abbastanza fine non sappiamo ricostruire la funzione
dell'enunciato, che è anche detta frequenza di
Nyquist. Quindi, da un punto di vista teorico, se il campionamento
è abbastanza fine non sappiamo ricostruire la funzione 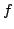 grazie alla (4.1).
grazie alla (4.1).
Da un punto di vista pratico questo ha dei limiti, intanto
bisogna supporre che le frquenze dell'immagine siano limitate, se
questo non è vero bisogn filtrare l'immagine a priori
convolvendo la 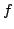 con una opportuna funzione, in maniera che le
frequenze troppo alte, fatta la trasformata, siano schiacciate a
zero; di conseguenza si perdono già informazioni in partenza. Ma
non c'è solo questo, i termini della successione che individua
con una opportuna funzione, in maniera che le
frequenze troppo alte, fatta la trasformata, siano schiacciate a
zero; di conseguenza si perdono già informazioni in partenza. Ma
non c'è solo questo, i termini della successione che individua
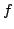 sono infiniti in quanto il supporto di
sono infiniti in quanto il supporto di 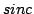 non è
limitato, quindi all'atto pratico questa formula non viene usata,
ma si convolve la
non è
limitato, quindi all'atto pratico questa formula non viene usata,
ma si convolve la 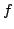 con una funzione "finestra" la cui
trasformata coinicida con quella di
con una funzione "finestra" la cui
trasformata coinicida con quella di  sul supporto di
sul supporto di
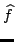 , ma che poi vada rapidamente a zero. In pratica
quindi non si può parlare di ricostruzione esatta, ma solo di
migliore o peggiore ricostruzione.
, ma che poi vada rapidamente a zero. In pratica
quindi non si può parlare di ricostruzione esatta, ma solo di
migliore o peggiore ricostruzione.



Next: Pulizia rumore
Up: Elaborazione Immagini: campionamento, aliasing
Previous: Teorema di campionamento shannon
Michele Cerulli
2000-10-29
 Il teorema di shannon ci dice come possiamo ricostruire la
funzione
Il teorema di shannon ci dice come possiamo ricostruire la
funzione