


Next: Teorema di campionamento shannon
Up: Elaborazione Immagini: campionamento, aliasing
Previous: Il campionamento
L'aliasing è un fenomeno strettamente legato al processo di
campionamento, e si può comprendere ragionando in termini di
trasformata di Fourier dell'immagine campionata 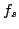 . Ulteriori esempi
di immagini in cui si possono osservare fenomeni di aliasing li
potete trovare nei libri e nei siti web indicati in bibliografia.
Un esempio sicuramente noto a tutti e quello che si può
osservare quando un personaggio della televisione indossa una
maglia a quadretti o striscie molto fitte si vede una strana
trama nel disegno della maglia. Il punto è che campionando in
maniera non adeguata l'immagine poi ricostruita pò apparire
alterata. Se dobbiamo ad esempio campionare
. Ulteriori esempi
di immagini in cui si possono osservare fenomeni di aliasing li
potete trovare nei libri e nei siti web indicati in bibliografia.
Un esempio sicuramente noto a tutti e quello che si può
osservare quando un personaggio della televisione indossa una
maglia a quadretti o striscie molto fitte si vede una strana
trama nel disegno della maglia. Il punto è che campionando in
maniera non adeguata l'immagine poi ricostruita pò apparire
alterata. Se dobbiamo ad esempio campionare 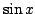 e lo
facciamo con passo
e lo
facciamo con passo 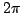 otterremo addirittura una funzione
costante, quindi una cosa che non c'era nella funzione iniziale,
abbiamo quindi un fenomeno di aliasing. Campionando la stessa
funzione con un altro passo potremmo ottenere una funzione
periodica ma di frequenza molto più bassa. Qui non si tratta
solo di perdere informazioni, ma di generare, nelle immagini
acquisite, "oggetti" che non erano presenti nell'immagine
originale.
otterremo addirittura una funzione
costante, quindi una cosa che non c'era nella funzione iniziale,
abbiamo quindi un fenomeno di aliasing. Campionando la stessa
funzione con un altro passo potremmo ottenere una funzione
periodica ma di frequenza molto più bassa. Qui non si tratta
solo di perdere informazioni, ma di generare, nelle immagini
acquisite, "oggetti" che non erano presenti nell'immagine
originale.
Il processo precedentemente introdotto di passaggio alle
trasformate di Fourier viene chiamato "Fourier Analysis", e ci
pò aiutare a capire meglio il problema dell'aliasing. Dal
confronto tra la trasformata
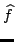 dell'immagine
originale, e la trasformata
dell'immagine
originale, e la trasformata
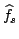 del suo
campionamento abbiamo visto che la seconda è una sommatoria
infinita di copie traslate della prima; in sostanza
del suo
campionamento abbiamo visto che la seconda è una sommatoria
infinita di copie traslate della prima; in sostanza
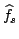 è una periodizzazione di
è una periodizzazione di
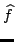 . Ora,
se il supporto di
. Ora,
se il supporto di
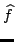 ha ampiezza minore del periodo di
ha ampiezza minore del periodo di
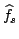 , tutto va bene, in quanto basta moltiplicare
, tutto va bene, in quanto basta moltiplicare
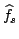 per un'apposita funzione a gradini e troviamo
per un'apposita funzione a gradini e troviamo
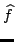 , quindi ricaviamo
, quindi ricaviamo 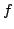 .
.
Se invece il supporto di
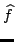 non è adeguatamente
limitato accade che le copie traslate si sovrappongono, per cui
non è più possibile ricostruire la funzione originale
non è adeguatamente
limitato accade che le copie traslate si sovrappongono, per cui
non è più possibile ricostruire la funzione originale 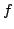 , a
partire da
, a
partire da
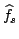 .
.
Ora, poichè il periodo di
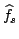 è strettamente in
relazione con la frequenza di campionamento, appare lecito che
sotto le adeguate ipotesi, si possa scegliere la frequenza di
campionamento in maniera da poter ricostruire
è strettamente in
relazione con la frequenza di campionamento, appare lecito che
sotto le adeguate ipotesi, si possa scegliere la frequenza di
campionamento in maniera da poter ricostruire 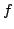 a partire da
a partire da
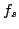 . A questo proposito ci viene in aiuto il Teorema di
Shannon.
. A questo proposito ci viene in aiuto il Teorema di
Shannon.



Next: Teorema di campionamento shannon
Up: Elaborazione Immagini: campionamento, aliasing
Previous: Il campionamento
Michele Cerulli
2000-10-29







