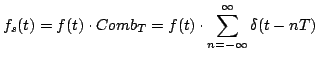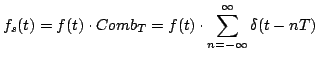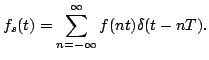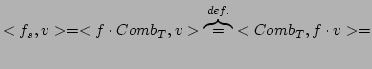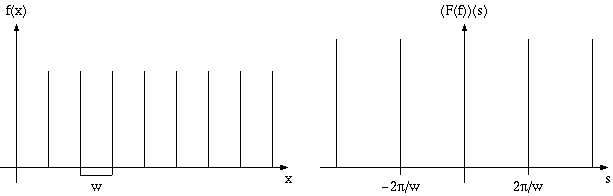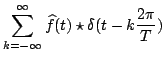Next: Aliasing
Up: Elaborazione Immagini: campionamento, aliasing
Previous: Introduzione
Come abbiamo già detto campionare (ing. ``sampling'') un'immagine
significa prenderne dei campioni, offero significa valutare 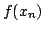 per una successione
per una successione 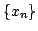 di valori del dominio di
partenza.
di valori del dominio di
partenza.
Ragionando in termini teorici si potrebbe tranquillamente
trattare di una successione infinata di valori.
Supponiamo ora di avere scelto di campionare la nostra immagine
(monodimensionale per semplicità di trattazione) con un passo 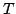 ,
questo significa che dalla successione
,
questo significa che dalla successione
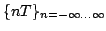 otteniamo la successione
otteniamo la successione 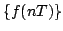 . Questa operazione,
matematicamente possiamo vederla come la moltiplicazione della
funzione
. Questa operazione,
matematicamente possiamo vederla come la moltiplicazione della
funzione 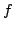 per la distribuzione
per la distribuzione
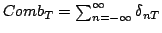 , quindi indicando con
, quindi indicando con
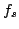 il campionamento di
il campionamento di 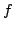 possiamo scrivere:
da cui
possiamo scrivere:
da cui
Purtroppo nella letteratura che ho trovato sulle questioni di
elaborazione immagini questa scrittura non viene chiarita bene, a mio
avviso si può interpretare 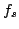 come una distribuzione in quanto
prodotto di una funzione
come una distribuzione in quanto
prodotto di una funzione 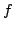 (con le dovute ipotesi di
integrabilità ) per una distribuzione
(con le dovute ipotesi di
integrabilità ) per una distribuzione 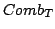 ; in effetti vale:
tale serie converge in quanto
; in effetti vale:
tale serie converge in quanto 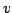 , come funzione test, ha supporto
compatto. Interpretare
, come funzione test, ha supporto
compatto. Interpretare 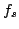 come prodotto ci servirà più
avanti, tuttavia, dalla letteratura, non è chiaro se
l'interpretazione che ho appena dato sia quella giusta.
come prodotto ci servirà più
avanti, tuttavia, dalla letteratura, non è chiaro se
l'interpretazione che ho appena dato sia quella giusta.
Il rapporto tra 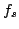 ed
ed 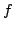 sarà l'argomento centrale di questo
seminario in quanto il problema fondamentale sarà ricorstruire
sarà l'argomento centrale di questo
seminario in quanto il problema fondamentale sarà ricorstruire 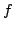 a
partire da
a
partire da 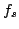 . Per affrontare tale questione ci sarà d'aiuto
una proprietà della trasformata di Fourier rispetto al prodotto di
convoluzione.
. Per affrontare tale questione ci sarà d'aiuto
una proprietà della trasformata di Fourier rispetto al prodotto di
convoluzione.
Convoluzione tra distribuzioni. Date due distribuzioni
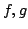 con
con 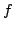 a supporto limitato, allora, per ogni funzione test
a supporto limitato, allora, per ogni funzione test 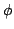
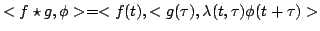 |
(2.1) |
dove 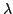 è una funzione test che vale 1 sul supporto di
è una funzione test che vale 1 sul supporto di
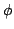 .
.
N.b.: Questa definizione, come quasi tutte quelle
relative alle distribuzioni, si ottiene estendendo una proprietà
della convoluzione sulle funzioni. Inoltre l'ipotesi che le due
distribuzioni abbiano supporto compatto è sovrabbondante, basta
che una sola verifichi tale proprietà per poter dare la
definizione. Infine, osserviamo che la convoluzione tra due
distribuzioni temperate è ancora temperata.
Trasformata di fourier di una funzione. Sia
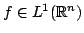 la sua trasformata
la sua trasformata
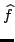 di Fourier è
data da:
di Fourier è
data da:
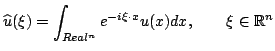 |
(2.2) |
In particolare si ha che
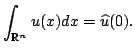 |
(2.3) |
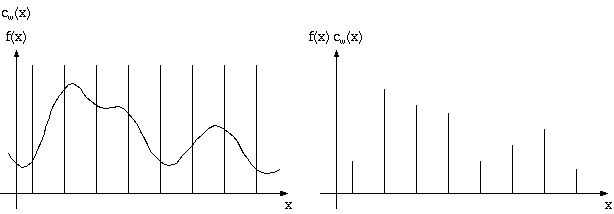
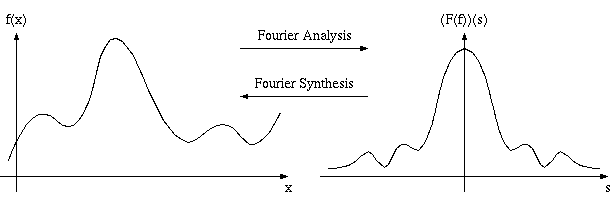
Nell'immagine mostriamo un esempio di trasformata.
Formula di inversione. Sia
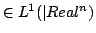 una funzione continua e limitata t.c.
una funzione continua e limitata t.c.
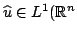 . Allora per ogni
. Allora per ogni
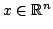 vale:
vale:
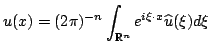 |
(2.4) |
da cui si scrive
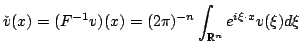 |
(2.5) |
Trasformata di fourier di una distribuzione. Data una
distribuzione temperata 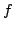 , allora
, allora
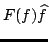 è ancora una
distribuzione temperata ed è data da:
è ancora una
distribuzione temperata ed è data da:
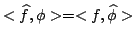 |
(2.6) |
Vale la formula di inversione:
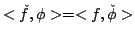 |
(2.7) |
Da cui abbiamo
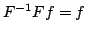 e
e
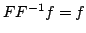 , per cui la trasformata è
bigettiva sullo spazio delle distribuzioni temperate.
, per cui la trasformata è
bigettiva sullo spazio delle distribuzioni temperate.
Alcune trasformate che ci saranno utili
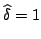 |
(2.8) |
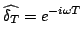 |
(2.9) |
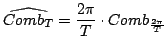 |
(2.10) |
dove
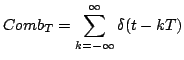 |
(2.11) |
Notiamo che
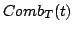 è una distribuzione temperata. Nella seguente immagina è possibile vedere la funzione Comb e la sua trafrormata di Fourier (a destra).
è una distribuzione temperata. Nella seguente immagina è possibile vedere la funzione Comb e la sua trafrormata di Fourier (a destra).
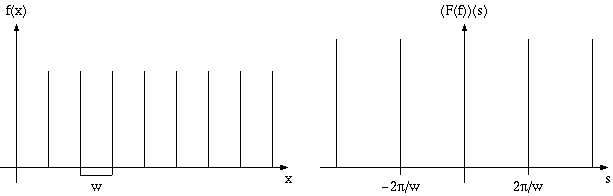
Teorema di convoluzione. Siano 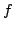 e
e 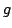 distribuzioni a
supporto limitato, allora
distribuzioni a
supporto limitato, allora
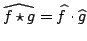 |
(2.12) |
Inoltre si ha che
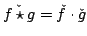 |
(2.13) |
Il teorema appena enunciato ha una pesante conseguenza sull'analisi
delle immagini digitalizzate. Torniamo alla questione del
campionamento, ed applichiamo il teorema per calcolare la trasformata
di Fourier di  :
Inoltre vale
:
Inoltre vale
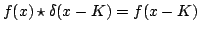 :
Di conseguenza possiamo interpretare
:
Di conseguenza possiamo interpretare
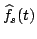 come una
sommatoria di copie traslate (di
come una
sommatoria di copie traslate (di
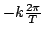 ) di
) di
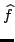 .
A questo punto appare chiaro come possa essere conveniente utilizzare
la trasformata di fourier per analizzare le immagini
digitalizzate. L'idea è di utilizzare la trasformata del
campionamento per risalire alla funzione vera e propria.
.
A questo punto appare chiaro come possa essere conveniente utilizzare
la trasformata di fourier per analizzare le immagini
digitalizzate. L'idea è di utilizzare la trasformata del
campionamento per risalire alla funzione vera e propria.
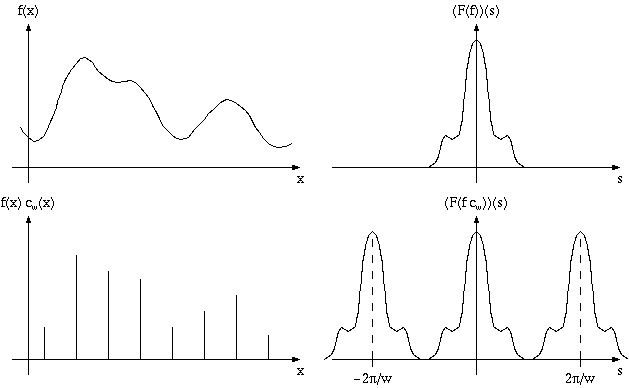
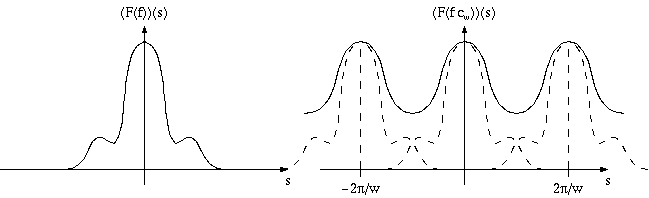
Bisogna
però fare attenzione, nell'immagine precedente le copie traslate
della trasformata non si sovrappongono (vedi immagine in basso), ma questa è un'eventualità
che può accadere. In tale caso non sarà possibile ricostruire la
funzione 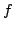 di partenza.
di partenza.



Next: Aliasing
Up: Elaborazione Immagini: campionamento, aliasing
Previous: Introduzione
Michele Cerulli
2000-10-29