


Next: Il campionamento
Up: Elaborazione Immagini: campionamento, aliasing
Previous: Elaborazione Immagini: campionamento, aliasing
Da un punto di vista matematico un'immagine in bianco e nero può
essere vista come una funzione
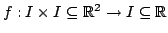 , dove
, dove
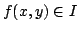 rappresenta il livello di grigio associato al punto
rappresenta il livello di grigio associato al punto
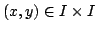 (abbiamo assunto che l'immagine sia quadrata).
Equivalentemente possiamo interpretare matematicamente suoni, immagini
a colori, immagini tridimensionali:
(abbiamo assunto che l'immagine sia quadrata).
Equivalentemente possiamo interpretare matematicamente suoni, immagini
a colori, immagini tridimensionali:
- Immagine a colori:
dove
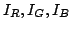 rappresentano rispettivamente i livelli di
rosso, verde e blu che costituiscono il color in un punto dell'immagine;
rappresentano rispettivamente i livelli di
rosso, verde e blu che costituiscono il color in un punto dell'immagine;
- Immagine tridimensionale (es. TAC):
- Immagine monodimensionale (ex. suono):
La versione digitalizzata di una immagine (ad esempio acquisita
con uno scanner), quella che effettivamente vediamo sul monitor,
interpretata nello stesso modo, appare come una funzione
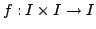 a gradini, dove l'alteza di ogni gradino corrisponde
all'intensità di grigio (per semplicità trattiamo immagini in
bianco e nero). In sostanza l'immagine originale viene suddivisa in
tanti quadratini (segmenti nel caso del suono) e si individua il
livello di grigio
a gradini, dove l'alteza di ogni gradino corrisponde
all'intensità di grigio (per semplicità trattiamo immagini in
bianco e nero). In sostanza l'immagine originale viene suddivisa in
tanti quadratini (segmenti nel caso del suono) e si individua il
livello di grigio 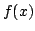 nel punto
nel punto 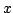 centrale di ogni quadratino. L'immagine
digitalizzata corrisponde quindi ad una matrice
centrale di ogni quadratino. L'immagine
digitalizzata corrisponde quindi ad una matrice 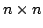 , se
l'immagine era quadrata ed era stata suddivisa in n*n quadratini,
dove i coefficenti corrispondo ai livelli di grigio
, se
l'immagine era quadrata ed era stata suddivisa in n*n quadratini,
dove i coefficenti corrispondo ai livelli di grigio 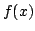 rilevati nei
rispettivi quadratini dell'immagine originale. Quando l'immagine viene
mostrata su uno schermo, essa viene ricostruita appunto come funzione
a gradini dando ad ogni quadratino il corrispondente livello di
grigio.
rilevati nei
rispettivi quadratini dell'immagine originale. Quando l'immagine viene
mostrata su uno schermo, essa viene ricostruita appunto come funzione
a gradini dando ad ogni quadratino il corrispondente livello di
grigio.
Appare subito evidente che in tutti questi passaggi molte informazioni
sull'immagine vanno persi. Intanto non vengono acquisiti tutti i
valori della funzione 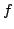 , ma solo un numero finito. Tanto più fine
è la duqadrettatura dell'immagine, tante più informazioni si
acquisiscono; di conseguenza si apre la questione di scegliere quanti
campioni della funzione acquisire in modo da ottenere una buona
rappresentazione senza troppi costi di computazione. L'ideale sarebbe
saper ricostruire tutta la funzione
, ma solo un numero finito. Tanto più fine
è la duqadrettatura dell'immagine, tante più informazioni si
acquisiscono; di conseguenza si apre la questione di scegliere quanti
campioni della funzione acquisire in modo da ottenere una buona
rappresentazione senza troppi costi di computazione. L'ideale sarebbe
saper ricostruire tutta la funzione
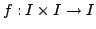 , ma
come vedremo questo è possibile solo in teoria.
, ma
come vedremo questo è possibile solo in teoria.
In questo seminario tentiamo di affrontare
il problema da un punto di vista teorico, ma cercando di enunciare i
risvolti pratici di quanto trovato. In particolare tratteremo un altro
tipo di ``errore'', ovvero l'aliasing, fenomeno per cui sull'immagine
acquisita si trovano ``oggetti'' non presenti in quella originale. Le
tecniche che enunceremo possono essere utilizzate anche per la pulizia
dell'immagine da ``rumori''.
Richiameremo gli strumenti matematici necessari via via che
serviranno. In particolare, dal punto di vista matematico tratteremo
il caso di immagini monodimensionali per smeplicità ; il caso a più
dimensioni può essere trattato in maniera analoga.



Next: Il campionamento
Up: Elaborazione Immagini: campionamento, aliasing
Previous: Elaborazione Immagini: campionamento, aliasing
Michele Cerulli
2000-10-29