Multi-Layer Networks (Reti a più strati)

Le mappe $M:\{0,1\}^{K}\rightarrow\{0,1\}$ che non possono essere realizzate con un singolo neurone, possono invece essere realizzate, almeno, con una rete feed-forward a due strati di neuroni di McCulloch-Pitts, con il secondo strato costituito da un solo neurone. Con rete feed-forward a strati si intende una rete di neuroni costituita più strati di neuroni dove l'input dei neuroni di uno strato proviene dai neuroni dello strato precedente, e l'output va verso lo strato successivo.
Iniziamo mostrando un esempio di come costruire il cosiddetto "grandmother neuron" che permette di realizzare operazioni non linearmente separabili, come XOR. L'insieme $\Omega^{+}$ su cui XOR vale 1 è:

$$\Omega^{+}=\{(1,0),(0,1)\}$$

Costruiamo una rete con la seguente struttura:

Input	I strato	II strato $\rightarrow Output$
	$y_{1}=\theta\left[W_{11}x_{1}+W_{21}x_{2}-V_{1}\right]$
$(x_{1},x_{2})$		$S((y_{1},y_{2}))=\theta\left[J_{1}y_{1}+J_{2}y_{2}-U\right]$
	$y_{2}=\left[W_{12}x_{1}+W_{22}x_{2}-V_{2}\right]$

Dobbiamo stabilire il valore dei parametri $W_{ij}$, $J_{k}$, $V_{k}$ e $U$ affinchè l'output corrisponda a quello di XOR. Inponendo le condizioni si possono trovare dei valori per cui la rete funziona, come ad esempio:

$$W_{11}=2 \qquad W_{12}=-2 \qquad V_{1}=1$$

$$W_{21}=-2 \qquad W_{22}=2 \qquad V_{2}=1$$

$$U=-\frac{1}{2} \qquad J_{1}=J_{2}=1$$

Per cui:

Input	I Strato	II Strato $\rightarrow Output$
	$y_{1}=\theta[2x_{1}-2x_{2}-1]$
$(x_{1},x_{2})$		$S((y_{1},y_{2}))=\theta\left[y_{1}+y_{2}-1/2\right]$
	$y_{2}=\theta[-2x_{1}+2x_{2}-1]$

Verifichiamo che la rete produca gli outputs richiesti:

$x=(x_{1},x_{2})$	$y=(y_{1},y_{2})$	$S(y)=\theta\left[y_{1}+y_{2}-1/2\right]$	$XOR(x_{1},x_{2})$
$(0,0)$	$(0,0)$	$\theta[0+0-1/2]=0$	0
$(1,0)$	$(1,0)$	$\theta[1+0-1/2]=1$	1
$(0,1)$	$(0,1)$	$\theta[0+1-1/2]=1$	1
$(1,1)$	$(0,0)$	$\theta[0+0-1/2]=0$	0

Cerchiamo ora di dare una costruzione generale che funzioni per inputs di dimensione qualsiasi e per operazioni qualsiasi. In particolare in questo modo proviamo che ogni operazione può essere realizzata con una rete a due strati di tipo feed-forward. Lo strato intermedio, quello i cui neuroni nell'esempio abbiamo chiamato $y_{1}$ e $y_{2}$, viene generalmente chiamato strato nascosto.

Costruzione. Sia $L$ la cardinalità dell'insieme $\Omega^{+}=\{x\in\{0,1\}^{K}\vert M(x)=1\}$, costruiamo i neuroni $y_{i}$ dello stato nascosto, che determinano se il vettore input $x$ appartiene ad $\Omega^{+}$; tali neuroni si chiamano anche "grandmother neurons". Iniziamo costruendo il blocco di base $G$:

$$x,x^{*}\in\{0,1\}^{K}:\quad G\left[x^{*};x\right]=\theta\left[\sum^{K}_{i=1}(2x_{i}-1)(2x^{*}_{i}-1)-K+1\right]$$ (6)

Input	I strato	II strato $\rightarrow Output$
	$y_{1}=\theta\left[\sum^{K}_{j=1}W_{1j}x_{j}-V\right]$
$(x_{1},...,x_{k})$	$\vdots$	$S((y_{1},...,y_{L}))=\theta\left[\sum^{L}_{i=1}J_{i}y_{i}-U\right]$
	$y_{L}=\left[\sum^{K}_{j=1}W_{Lj}x_{j}-V\right]$

Proposizione: $G\left[x^{*};x\right]=1\quad\Leftrightarrow\quad x=x^{*}$
Dimostrazione:

Iniziamo dimostrando che $G\left[x^{*};x\right]=1\quad\Leftarrow\quad x=x^{*}$

$$G\left[x;x\right]=\theta\left[\sum^{K}_{i=1}(2x_{i}-1)^{2}-K+1\right]=\theta\left[\sum^{K}_{i=1}1-K+1\right]=1$$

Quindi mostriamo com $x\neq x^{*}\Rightarrow G\left[x^{*};x\right]=0$:

$$\forall x_{i},x^{*}_{i}\in\{0,1\}:\qquad (2x_{i}-1)(2^{*}_{i... ...{*}_{i} \\ -1\quad se \quad x_{i}\neq x^{*}_{i} \end{array}$$

Per cui:

$$\sum^{K}_{i=1}(2x_{i}-1)(2x^{*}_{i}-1)=K-2\times n$$

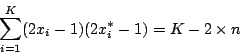
dove $n$ è il numero degli indici $i$ tali che $x_{i}\neq x^{*}_{i}$, da cui segue:

$$x\neq x^{*}\Rightarrow \sum^{K}_{i=1}(2x_{i}-1)(2x^{*}_{i}-1)\leq K-2$$

$$\Rightarrow G\left[x^{*};x\right]\leq \theta[K-2-K+1]=\theta[-1]=0 \Rightarrow G\left[x^{*};x\right]=0$$

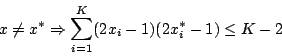
La dimostrazione è completata.

Fissato $x^{*}$, l'espressione $G[x^{*};x]$, può essere interpretata come una operazione effettuata sulla variabile $x$, e come tale, è della forma McCulloch-Pitts:

$$G\left[x^{*};x\right]=\theta\left[2\sum^{K}_{i=1}(2x^{*}_{i}-1)x_{i}-2\sum^{K}_{i=1}x^{*}+1\right]$$

Un neurone costruito in questo modo restituisce 1 se l'input è in $\Omega^{+}$, altrimenti restituisce zero. Possiamo quindi realizzare lo strato nascosto di neuroni nel seguente modo:

$$\Omega^{+}=\{x\in\{0,1\}^{K}\mid M(x)=1\}=\{x^{1},...,x^{L}\}$$

$$\forall i\in \{1,...L\}:\qquad y_{i}:\{0,1\}^{K}\rightarrow\{0,1\},\qquad y_{i}=G\left[x^{i};x\right]$$

In questo modo, se $x\in\Omega^{+}$ allora uno, ed uno solo dei neuroni $y_{i}$ dello strato nascosto produce 1 come output, se invece $x$ non è in $\Omega$ allora tali neuroni hanno tutti un output nullo. A questo punto, per completare la rete, basta realizzare un ultimo strato costituito da un neurone $S(y)$ che non fa altro che verificare se uno degli $y_{i}$ è "eccitato" oppure no, nel primo caso produce output 1, altrimenti produce 0. In questo modo l'output della rete è 1 se e solo se il vettore input $x$ sta in $\Omega^{+}$. Un esempio funzionante è il seguente, tenuto conto che gli $y_{i}$ sono diversi da zero solo uno alla volta:

$$y_{i}=\theta\left[\sum^{K}_{j=1}W_{ij}x_{j}-V\right] \qquad S(y)=\theta\left[\sum^{L}_{i=1}y_{i}-\frac{1}{2}\right]$$

$$W_{ij}=2\left(2x^{i}_{j}-1\right),\qquad V=2\sum^{K}_{j=1}x^{i}_{j}-1$$

Poichè questa costruzione può essere realizzata per un $\Omega^{+}$ qualsiasi, e poichè tale insieme caratterizza l'operazione che lo definisce, abbiamo che:

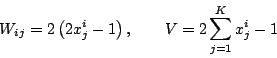
Tutte le operazioni $M:\{0,1\}^{K}\rightarrow\{0,1\}$ possono essere realizzate da una rete a due strati di tipo feed-forward, con neuroni di McCulloch-Pitts.

Dato che la cardinalità di $\Omega^{+}$ è dell'ordine di $2^{K}$, e che tale cardinalità corrisponde al numero di neuroni necessari per realizzare lo strato nascosto, ne risulta che questo metodo non è particolarmente efficiente, ma è servito per dimostrare l'universalità del tipo di reti e di neuroni in questione.

Inserisci i termini di ricerca

Web	www.mkvale.it

Invia modulo di ricerca