|
|
|
|||||||
| 0 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 |
| 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
|
|
|
|||||||
| 0 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 |
| 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
|
|
XOR(x,y) | |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Supponiamo che invece una tale terna esista, allora:Le tre condizioni, dettate dalla tavola di verità di XOR, non possono essere tutte verificate allo stesso tempo, da cui segue la validità della proposizione. Per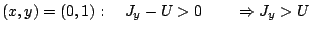
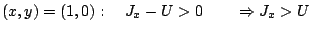
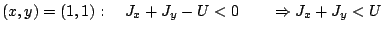
possiamo costruire esempi simili applicando XOR alle prime due variabili d'input:
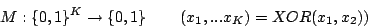
Di conseguenza sappiamo cheoperazioni che non possono essere realizzate con un singolo neurone di McCulloch-Pitts. Per analizzare il problema e capire quali operazioni possono essere realizzate con un singolo neurone possiamo dare un'interpretazione un po' più geometrica della situazione. Tanto per cominciare, il numero totale delle operazioni è:
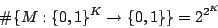
L'insiemedei possibili vettori input corrisponde ai vertici dell'ipercubo unitario in
, mentre il neurone che esegue l'operazione
![\begin{displaymath}S:\{0,1\}^{K}\rightarrow\{0,1\}\qquad S(x)=\theta\left[\sum^{K}_{k=1}J_{k}x_{k}-U\right]\end{displaymath}](img160.png)
può essere interpretato come operatore che dividein due sottospazi separati dall'iperpiano
. L'informazione che otteniamo dal neurone, quindi, è semplicemente in quale sottospazio di
si trova un dato vettore input
. Questa suddivisione in sottospazi, in realtà, corrisponde a quella già introdotta precedentemente dell'insieme
in
e
: l'insieme dei vertici dell'ipercubo per cui vale
corrisponde ad
, mentre l'insieme dei vertici su cui
vale
è
. Poichè ciascuna delle
operazioni è univocamente identificata dall'insieme
, è possibile rappresentare ciascuna di esse disegnando l'ipercubo, colorando di nero i vertici appartenenti ad
, e di bianco quelli appartenenti ad
.
Perl'ipercubo è un segmento con 2 vertici, 4 sono le operazioni
possibili, ovvero 4 modi di colorare i vertici:
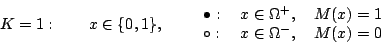

Perl'ipercubo è un quadrato e ci sono
operazioni
, 16 modi di colorare i quattro vertici del quadrato:
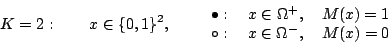






Per

l'ipercubo è un cubo, con 8 vertici, per cui ci sono
operazioni
, 256 modi di colorare i vertici del cubo.
Ricordandoci che il neurone di McCulloch-Pitts dividein due semispazi con un iperpiano, risulta chiaro che, di tutte le operazioni elencate negli esempi, esso può eseguire solo quelle per cui
ed
possono essere separati con un singolo iperpiano
. Operazioni che godono di tale caratteristica si chiamano linearmente separabili.
Rivedendo gli esempi sopra rappresentati appare chiaro come persia sempre possibile separare i vertici neri da quelli bianchi con un singolo iperpiano, mentre per
esistono due operazioni per cui questo non è possibile:
Le due operazioni in questione sono esattamente

e
:
Nel prossimo paragrafo vedremo come si possono eseguire tali operazioni, utilizzando più di un neurone di McCulloch-Pitts.
0 0 0 0 1 1 1 0 1 1 1 0
0 0 1 0 1 0 1 0 0 1 1 1



Next: Multi-Layer Networks (Reti a Up: Layered Networks Previous: Layered Networks Michele Cerulli 2000-10-29