L'universalità dei neuroni di McCulloch-Pitts

In questa sezione mostreremo che il più semplice modello di neurone è in realtà già universale, nel senso che una qualsiasi macchina che processa informazioni digitali può essere emulata da una rete, propriamente costruita, di tali neuroni. Poichè tutte le unità logiche principali delle macchine digitali possono essere costruite con neuroni di McCulloch-Pitts, tutti i teoremi dell'informatica (computabilità, macchine di Turing) che valgono per tali macchine, valgono anche per le reti di neuroni di McCulloch-Pitts. In questa sede ci limitiamo ad analizzare alcune semplici proposizioni.
Riduzione ad Operazioni Binarie di tipo Single-Output: ogni macchina digitale (finita?) può essere ridotta ad una collezione di macchine binarie con un solo output (Single-Output Binary Machines):

• Tali macchine possono gestire solo rappresentazioni finite di numeri reali, per cui:
  $\pi\rightarrow3.141592653589793238462643$
  Ogni tale rappresentazione finita (numeri a precisione finita) può essere rappresentato da un numero finito di interi:
  $\pi\rightarrow(\overbrace{3.141592653589793238462643}^{cifre};\overbrace{1}^{virgola})$
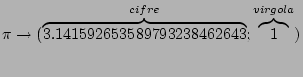
  Ogni intero, infine, si può esprimere come una stringa di numeri binari $\in\{0,1\}$:
  $(10011010111)=1\cdot2^{10}+0\cdot2^{9}+0\cdot2^{8}+1\cdot2^{7}+1\cdot2^{6}+0\cdot2^{5}+1\cdot2^{4}+0\cdot2^{3}+1\cdot2^{2}+1\cdot2^{1}+1\cdot2^{0}$ =1024+128+64+16+4+2+1=1239
• Ogni macchina può essere considerata come un'applicazione che mappa dei vettori binari di dimensione finita $\textbf{S}\in\Omega\subseteq\{0,1\}^{k}$(che può rappresentare caratteri, numeri, tasti della tastiera, qualsiasi cosa) su altri vettori binari finiti di output $\textbf{S}\in\Omega\subseteq\{0,1\}^{k}$. Le macchine deterministiche risponderanno, per definizione, sempre esattamente nello stesso modo ad inputs identici. Per cui ogni macchina deterministica finita può essere descritta dettagliatamente specificando il vettore di output S'(S) per ogni possibile vettore input $\textbf{S}\in\Omega$, ovvero specificando l'applicazione M:
  $M:\Omega\rightarrow\{0,1\}^{k}$                  $M\textbf{S}=\textbf{S'}(\textbf{S})\forall\textbf{S}\in\Omega$
• Infine possiamo sempre considerare K sottomacchine indipendenti $M_{\ell}(\ell=1,...,K)$ tali che ciascuna di esse rappresenti l'elemento $\ell$ del vettore output della mappa M, che è quindi rappresentata dall'insieme delle sottomappe:
  
  $M\ell:\Omega\rightarrow\{0,1\}$                 $M_{\ell}\textbf{S}=S^{\prime}_{\ell}(\textbf{S})\forall\textbf{S}\in\Omega$

A questo punto ci possiamo chiedere se è possibile ottenere tutte queste mappe $M:\Omega\subseteq\{0,1\}^{N}\rightarrow\{0,1\}$ tramite reti di neuroni di McCulloch-Pitts. Per rispondere a questa domanda semplifichiamo ulteriormente il problema mostrando che ogni mappa di questo tipo si può ottenere tramite tre operazioni logiche di base: $\{\wedge,\vee,\neg\}$.

Riduzione a Tre Operazioni Elementari. Iniziamo riducendo il problema ulteriormente. Consideriamo la seguente partizione di $\Omega$ dipendente dall'output del vettore:

$$\Omega=\Omega^{+}\cup\Omega^{-} \qquad \Omega^{+}=\{\... ...qquad \Omega^{-}=\{\textbf{S}\in\Omega\vert M\textbf{S}=0\}$$ (5)

A questo punto numeriamo gli elementi di $\Omega^{+}$, tenendo conto che $p=\char93 \Omega\leq N$, in quanto $\Omega\subseteq\{0,1\}^{N}$.

$\Omega^{+}=\{S^{1},...,S^{p-1},S^{p}\}$         $S^{\mu}\in\{0,1\}^{N}$

Tramite l'introduzione dei tre operatori logici $\wedge(AND),\vee(OR),\neg(NOT)$, definiti dalle relative tavole di output (tavole di verita!),

$\wedge:{0,1}_{2}\rightarrow{0,1}$         

x y	x$\wedge$y
0 0	0
0 1	0
1 0	0
1 1	1

x y	x$\vee$y
0 0	0
0 1	1
1 0	1
1 1	1

         $\vee:{0,1}_{2}\rightarrow{0,1}$
$\neg:{0,1}_{2}\rightarrow{0,1}$        

x	$\neg$x
0	0
1	1

realizziamo l'operatore $SAME(x,y)$, che ci dice quando due variabili arbitrarie hanno lo stesso valore:

$SAME(x,y)=(x\wedge y)\vee((\neg x)\wedge(\neg y))$

Gli operatori AND e OR possono essere estesi ad inputs di più di due variabili nel modo standard:

$x_{1}\wedge x_{2}\wedge...\wedge x_{L-1}\wedge x_{L}:=x_{1}\wedge(x_{2}\wedge(...\wedge(x_{1}\wedge x_{L})...))$
$x_{1}\vee x_{2}\vee...\vee x_{L-1}\vee x_{L}:=x_{1}\vee(x_{2}\vee(...\vee(x_{1}\vee x_{L})...))$

A questo punto, data la mappa ad output singolo $M:\Omega\subseteq\{0,1\}^{N}\rightarrow\{0,1\}$, una macchina che la esegue può essere costruita, dati $\Omega_{+}$ e il vettore input $\textbf{S}$, tramite l'operatore SAME. La macchina semplicemente se $\textbf{S}$ è identico ad uno dei vettori di $\Omega_{+}$, in tal caso l'output sarà 1, altrimenti sarà 0:

$M\textbf{S}= \{ \begin{array}{c} 1\quad se\quad S\in\Omega^{+} \\ 0\quad se\quad S\in\Omega^{-} \end{array}$

Che in termini delle operazioni logiche SAME, $\wedge$, $\vee$ e $\neg$, si esprime:

$M\textbf{S}=\left(SAME(S_{1},S^{1}_{1})\wedge SAME(S_{2},S^{1}_{2})\wedge...\w... ...})\wedge...\wedge SAME(S_{N-1},S^{2}_{N-1})\wedge SAME(S_{N},S^{2}_{N})\right)$
$\vdots$ $\left(SAME(S_{1},S^{1}_{1})\wedge SAME(S_{2},S^{p-1}_{2})\wedge...\wedge SAME... ...})\wedge...\wedge SAME(S_{N-1},S^{p}_{N-1})\wedge SAME(S_{N},S^{p}_{N})\right)$

Quest'ultima espressione può essere costruita utilizzando solo le operazioni di base $\{\wedge,\vee,\neg\}$, di conseguenza ogni operazione $M:\Omega\subseteq\{0,1\}^{N}\rightarrow\{0,1\}$, quindi ogni operazione di una qualsiasi macchina digitale finita deterministica, può essere ridotta alla combinazione di tali operazioni di base.
Possiamo ridurre ulteriormente l'insieme di operazioni in quanto $\vee$ (OR) può essere scritta in termini di $\neg$ (NOT) e $\wedge$ (AND):

$x\vee y=\neg((\neg x)\wedge(\neg y))$

$x$	$y$	$x\vee y$	$\neg x$	$\neg y$	$(\neg x)\wedge (\neg y)$
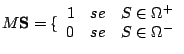
0	0	0	1	1	1
0	1	1	1	0	0
1	0	1	0	1	0
1	1	1	0	0	0

Infine possiamo addirittura ridurre l'insieme delle operazioni di base ad uno, definendo NAND (NOT-AND), come la negazione di $\wedge$ (AND), per cui:

• $\neg x=NAND(x,x)$
• $x\wedge y=NAND(NAND(x,y),NAND(x,y))$

$x$	$y$	$NAND(x,y)$	$NAND((NAND(x,y),NAND(x,y))$
0	0	1	0
0	1	1	0
1	0	1	0
1	1	0	1

$x$	$NAND(x,x)$
0	1
1	0

Realizzazione di Operazioni Elementari con i Neuroni di McCulloch-Pitts. Mostriamo come è possibile, tramite un solo neurone di questo tipo, realizzare le operazioni elementari di base. Per dimostrare l'universalità di tali neuroni basterebbe realizzare l'operazione NAND, comunque mostriamo come si possono realizzare anche le $\{\wedge,\vee,\neg\}$. Ricordiamo che il modello è:

$$S_{i}(t+\Delta )=\theta \left[ \sum ^{N}_{k=1}J_{ik}S_{k}(t)-U_{i}^{*}\right]$$

Prendiamo in considerazione un neurone che riceve due inputs (uno solo nel caso di $\neg$) $S_{1}=x$ e $S_{2}=y$ ( $x,y \in \{0,1\}$, per il quale possiamo scegliere come definire la soglia $U^{*}$ ed i pesi $J_{1}$, $J{2}$; tenendo conto di dover definire, per ciascun tipo di operazione, la soglia ed i pesi, il modello specifico che consideriamo è:

$$S(t+\Delta )=\theta \left[ \sum ^{2}_{k=1}J_{k}S_{k}(t)-U^{*}\right]=\theta \left[J_{1}x+J_{2}y-U^{*}\right]$$

$$\theta(z)=1 \quad per \quad z>0;$$

$$\theta(z)=0 \quad per \quad z\leq0;\\$$

Le operazioni di cui sopra possono quindi essere realizzate:

$J_{1}=1, J_{2}=1,U^{*}=\frac{3}{2}$    

$x$	$y$	$x\wedge y$	$x+y-3/2$	$\theta\left[x+y-3/2\right]$
0	0	0	-3/2	0
0	1	0	-1/2	0
1	0	0	-1/2	0
1	1	1	1/2	1

$J_{1}=1, J_{2}=1,U^{*}=\frac{1}{2}$    

$x$	$y$	$x\vee y$	$x+y-1/2$	$\theta\left[x+y-1/2\right]$
0	0	0	-1/2	0
0	1	1	1/2	1
1	0	1	1/2	1
1	1	1	3/2	1

$J_{1}=-1, U^{*}=-\frac{1}{2}$    

$x$	$\neg x$	$-x+1/2$	$\theta\left[-x+1/2\right]$
0	1	1/2	1
1	0	-1/2	0

$J_{1}=-1, J_{2}=-1,U^{*}=-\frac{3}{2}$    

$x$	$y$	$NAND(x,y)$	$-x-y+3/2$	$\theta\left[-x-y+3/2\right]$
0	0	1	3/2	1
0	1	1	1/2	1
1	0	1	1/2	1
1	1	0	-1/2	0

Inserisci i termini di ricerca

Web	www.mkvale.it

Invia modulo di ricerca