S dipende dal potenziale interno V(t) del neurone da una funzione: il neurone al momento t è eccitato, quindi produce un output;
: il neurone al momento t non è eccitato, quindi non produce alcun output;
JIl ``messaggio'' passato da k ad i lo esprimiamo con J> 0: la sinapsi che connette i due neuroni è eccitativa, ovvero favorisce il passaggio di informazioni; J
< 0: la sinapsi è inibitoria.
VGeneralmente la funzione f si assume essere una sommatoria, per cui le due equazioni diventano del tipo:=
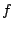
; S
=
=
;
Dove:: sinapsi che connette k
i
: tempo impiegato dal segnale nel tratto k
i
: successo o fallimento della trasmissione del messaggio k
i
: output del neurone (firing state)
: potenziale del neurone
: soglia di ``fuoco'' del potenziale del neurone, oltre la quale il messaggio viene trasmesso
: costanti dovute alle proprietà elettriche del neurone, che assumiamo uguali per tutti i neuroni.
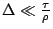
Tramite appositi conti e considerazioni di tipo probabilistico sulle variabili casualie
possiamo giungere alla seguente equazione:
dove:![\( g\left[ x\right] =\int ^{*}_{-\infty }P(u)du \)](img31.png)
con
A partire da qui è possibile ricavare la maggior parte dei modelli di neuroni, ne elenchiamo qualcuno:
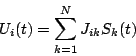
Poichè in questo modo abbiamo perso tutte le variabili legate al tempo, è necessario recuperare in qualche modo la dinamicità del modello descrivendo lo statodel neurone in funzione del valore precedente del potenziale post-sinaptico
:
Il tempo ora è discretizzato in unità di periodoed otteniamo il modello di McCulloch-Pitts:
![\begin{displaymath}
S_{i}(t+\Delta )=\theta \left[ \sum ^{N}_{k=1}J_{ik}S_{k}(t)-U_{i}^{*}\right] \end{displaymath}](img49.png)
Nonostante la sua semplicità questo tipo di modello è universale, nel senso che, costruendone apposite reti, permette di emulare le operazioni di una qualsiasi macchina di Turing finita, nel prossimo paragrafo ci occuperemo proprio di questo. Osserviamo inoltre che si può ottenere questo modello anche senza partire dalle equazioni sopra costruite, ma semplicemente scegliendo di modellizzare un neurone come:
un struttura caratterizzata da un output, un insieme di pesi, ed un insieme di inputs. L'output del neurone i lo indichiamo con; gli inputs sono dati dal prodotti degli outputs di altri neuroni e dei pesi
che determinano la portata del collegamento dal neurone j verso il neurone i. Il potenziale del neurone viene preso come la sommatoria degli inputs ricevuti più una costante
. A questo punto, poichè assumiamo che un neurone si ecciti e quindi trasmetta un messaggio quando il suo potenziale supera una certa soglia, possiamo ottenere il modello sopra descritto scegliendo un'apposita
. Nel caso, ad esempio, che
sia una funzione a gradini (es
per
,
per
), abbiamo che l'output del neurone sarà diverso da zero solo se la somma degli inputs è sufficientemente alta, e la costante
stabilisce quanto alta questa somma debba essere, insomma stabilisce la ``soglia di fuoco'' del neurone.
L'idea è che se le fasidei neuroni sono identiche (
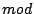
), i potenziali dei neuroni oscillano in maniera coordinata, per cui il potenziale del neurone subisce l'influenza degli inputs ricevuti da altri neuroni, altrimenti oscilla con una propria frequenza
. Le sinapsi eccitatorie devono indurre maggiore coerenza tra due neuroni, mentre quelle inibitorie devono tendere a scordinare i due neuroni. Il più semplice modello gode di tali proprietà è il seguente: