Altri Seminari
Next: About this document ...
Cenni sulle reti neurali
Michele Cerulli
Date: 19 Luglio 2000
V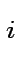 =
= 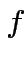
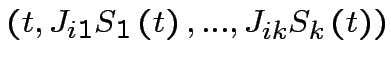 ;
;
S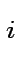 =
=
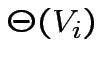 =
=
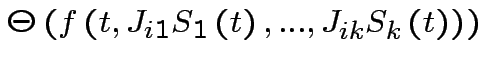 ;
;
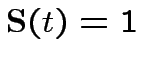 : il neurone al momento t è eccitato,
quindi produce un output;
: il neurone al momento t è eccitato,
quindi produce un output;
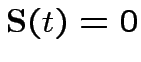 : il neurone al momento t non è eccitato,
quindi non produce alcun output;
: il neurone al momento t non è eccitato,
quindi non produce alcun output;
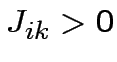 : la sinapsi che connette i due neuroni è
eccitativa, ovvero favorisce il passaggio di informazioni;
: la sinapsi che connette i due neuroni è
eccitativa, ovvero favorisce il passaggio di informazioni;
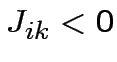 : la sinapsi è è inibitoria.
Il modello di McCulloch-Pitts
: la sinapsi è è inibitoria.
Il modello di McCulloch-Pitts
Esempi di altri modelli: equazione generale
dove:
con 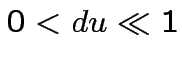 Graded Response Neurons. Si assume che la trasmissione
del messaggio avvenga istantaneamente,
Graded Response Neurons. Si assume che la trasmissione
del messaggio avvenga istantaneamente,
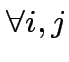 , e si trascurano i termini direset,
assumendo che le fluttuazioni del potenziale successive alla
trasmissione del messaggio siano irrilevanti:
, e si trascurano i termini direset,
assumendo che le fluttuazioni del potenziale successive alla
trasmissione del messaggio siano irrilevanti:
![$ g\left[ U-U^{*}\right] =\int ^{U-U^{*}}_{-\infty }P(u)du $](img23.png)
Coupled oscillators.
L'universalità dei neuroni di McCulloch-Pitts
Tali neuroni sono universali nel senso che permettono di emulare
una qualsiasi macchina digitale finita.
Riduzione ad operazioni binarie con output singolo:
Come possiamo ottenere le mappe
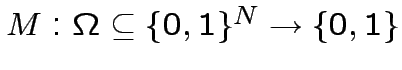 con i neuroni di
McCulloch-Pitts?
con i neuroni di
McCulloch-Pitts?
Riduciamo ulteriormente il problema...
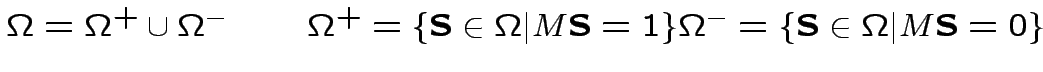
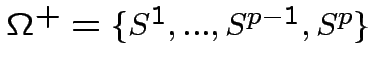
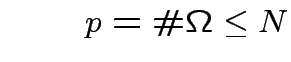
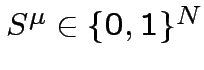
Tramite gli operatori
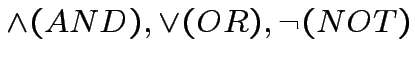 , definiamo
l'operatore
, definiamo
l'operatore 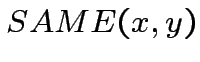 , che dice quando due variabili arbitrarie
hanno lo stesso valore:
, che dice quando due variabili arbitrarie
hanno lo stesso valore:
Data la mappa ad output singolo
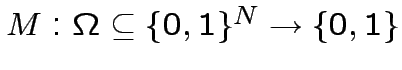 , una macchina
che la esegue può essere costruita, dati
, una macchina
che la esegue può essere costruita, dati
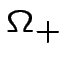 e il
vettore input
e il
vettore input
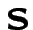 , tramite l'operatore SAME. La macchina
verifica se
, tramite l'operatore SAME. La macchina
verifica se
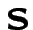 è identico ad uno dei vettori di
è identico ad uno dei vettori di
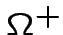 , in tal caso l'output sarà 1, altrimenti
sarà 0:
, in tal caso l'output sarà 1, altrimenti
sarà 0:
Che in termini delle operazioni logiche SAME, 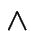 ,
, 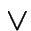 e
e
 , si esprime:
, si esprime:
Realizzazione di Operazioni Elementari con i Neuroni di
McCulloch-Pitts.
Bisogna stabilire i
valori di 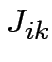 e
e 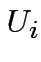 .
.
Esempio: neurone che riceve due inputs 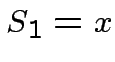 e
e
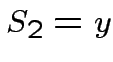 (
(
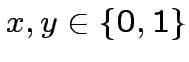 ).
).
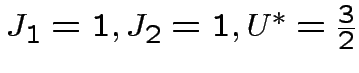
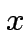 |
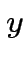 |
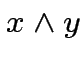 |
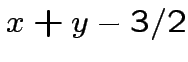 |
![$ \theta\left[x+y-3/2\right]$](img66.png) |
| 0 |
0 |
0 |
-3/2 |
0 |
| 0 |
1 |
0 |
-1/2 |
0 |
| 1 |
0 |
0 |
-1/2 |
0 |
| 1 |
1 |
1 |
1/2 |
1 |
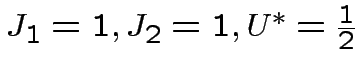
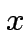 |
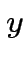 |
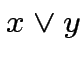 |
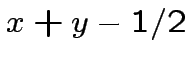 |
![$ \theta\left[x+y-1/2\right]$](img70.png) |
| 0 |
0 |
0 |
-1/2 |
0 |
| 0 |
1 |
1 |
1/2 |
1 |
| 1 |
0 |
1 |
1/2 |
1 |
| 1 |
1 |
1 |
3/2 |
1 |
Apprendimento
Regola di Hebb: le informazioni vengono immagazzinate
sotto forma di "forza" delle sinapsi che connettono i neuroni;
apprendere significa modificare tali sinapsi.
Il Perceptrone
"Apprendere" significa modificare i parametri 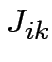 ed
ed
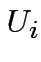
Dato un insieme "insegnante"
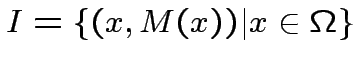
si sceglie un elemento a caso in 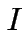 , se
, se
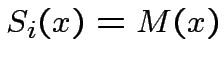 si
lascia tutto inalterato, altrimenti si modificano i parametri
caratterizzanti il neurone studente
si
lascia tutto inalterato, altrimenti si modificano i parametri
caratterizzanti il neurone studente 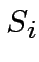 .
Problema Può il Perceptrone imparare ad eseguire una
qualsiasi operazione?
.
Problema Può il Perceptrone imparare ad eseguire una
qualsiasi operazione?
Nel 1969 Papert mostra che in effetti questo non è vero, basta
costruire degli appositi esempi.
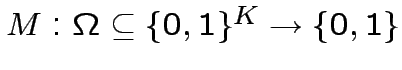
Per K=1
Per 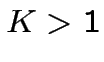 un solo neurone non basta, ad esempio, per eseguire
XOR(x,y):
un solo neurone non basta, ad esempio, per eseguire
XOR(x,y):
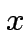 |
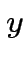 |
XOR(x,y) |
| 0 |
0 |
0 |
| 0 |
1 |
1 |
| 1 |
0 |
1 |
| 1 |
1 |
0 |
Proposizione:Non esiste alcuna terna di numeri
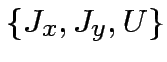 tali che:
Dimostrazione:
Supponiamo che invece una tale terna
esista, allora:
Separabilità lineare
tali che:
Dimostrazione:
Supponiamo che invece una tale terna
esista, allora:
Separabilità lineare
L'insieme
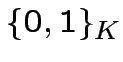 dei possibili vettori input corrisponde
ai vertici dell'ipercubo unitario in
dei possibili vettori input corrisponde
ai vertici dell'ipercubo unitario in 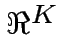 , mentre il neurone
che esegue l'operazione
, mentre il neurone
che esegue l'operazione
può essere interpretato come operatore che divide 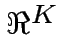 in
due sottospazi separati dall'iperpiano
in
due sottospazi separati dall'iperpiano
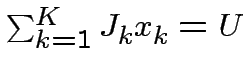
Per 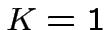 :
Per
:
Per 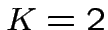 l'ipercubo è un quadrato e ci sono
l'ipercubo è un quadrato e ci sono
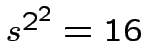 operazioni
operazioni
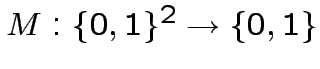 , 16 modi di colorare
i quattro vertici del quadrato:
, 16 modi di colorare
i quattro vertici del quadrato:
per 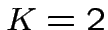 esistono due operazioni per cui questo non è possibile:
Le due operazioni in questione sono esattamente
esistono due operazioni per cui questo non è possibile:
Le due operazioni in questione sono esattamente 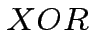 e
e 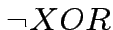 :
Multi-Layer Networks (Reti a più strati)
:
Multi-Layer Networks (Reti a più strati)
Reti
feed-forward a due strati di neuroni di McCulloch-Pitts,
con il secondo strato costituito da un solo neurone.
"Grandmother neuron" che realizzi XOR.
Costruiamo una rete con la seguente struttura:
dove:
![$ y_{1}=\theta\left[W_{11}x_{1}+W_{21}x_{2}-V_{1}\right]$](img127.png)
![$ y_{2}=\left[W_{12}x_{1}+W_{22}x_{2}-V_{2}\right]$](img128.png)
![$ S((y_{1},y_{2}))=\theta\left[J_{1}y_{1}+J_{2}y_{2}-U\right]$](img129.png) Per cui:
La rete produce gli outputs richiesti:
Per cui:
La rete produce gli outputs richiesti:
Costruzione.
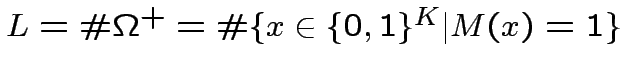
Dove:
![$ y_{i}=\theta\left[\sum^{K}_{j=1}W_{ij}x_{j}-V\right]$](img148.png)
![$ S((y_{1},...,y_{L}))=\theta\left[\sum^{L}_{i=1}J_{i}y_{i}-U\right]$](img149.png)
Costruiamo il blocco di base 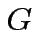 :
:
Proposizione:
![$ G\left[x^{*};x\right]=1\quad\Leftrightarrow\quad x=x^{*}$](img153.png)
Dimostrazione:
![$ \bullet\quad G\left[x^{*};x\right]=1\quad\Leftarrow\quad
x=x^{*}$](img154.png)
![$ \bullet\quad x\neq x^{*}\Rightarrow
G\left[x^{*};x\right]=0$](img157.png) :
Fissato
:
Fissato 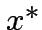 , l'espressione
, l'espressione
![$ G[x^{*};x]$](img163.png) , interpretata come
una operazione effettuata sulla variabile
, interpretata come
una operazione effettuata sulla variabile 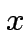 è della forma
McCulloch-Pitts:
è della forma
McCulloch-Pitts:
Un neurone costruito in questo modo restituisce 1 se l'input è in
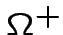 , altrimenti restituisce zero.
Strato nascosto di neuroni:
, altrimenti restituisce zero.
Strato nascosto di neuroni:
Costruendo l'ultimo strato otteniamo la rete:
L'apprendimento: il Perceptrone
Data l'operazione
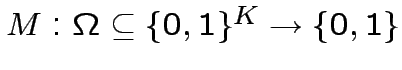
passo
1:Scegliere una domanda a caso, ovvero un
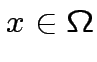 qualsiasi.
qualsiasi.
passo 2:Controllare se "studente" ed "insegnante" sono
d'accordo:
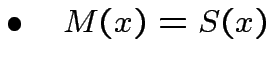 : torna al passo 1
: torna al passo 1
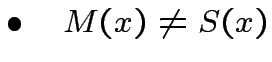 : modifica parametri e torna al passo 1
: modifica parametri e torna al passo 1
modifica parametri:
![$ J\quad\rightarrow\quad J+\Delta J[J,U;x,M(x)]$](img174.png)
![$ U\quad\rightarrow\quad U+\Delta U[J,U;x,M(x)]$](img175.png)
Definizione:
si dice perceptrone un neurone "studente" di
McCulloch-Pitts che impara secondo la regola di apprendimento:
modifica parametri:
![$ J\quad\rightarrow\quad J+\Delta J[J,U;x,M(x)]$](img174.png)
![$ U\quad\rightarrow\quad U+\Delta U[J,U;x,M(x)]$](img175.png)
Domande:
- Un perceptrone può apprendere come eseguire una qualsiasi
operazione?
- La procedura di apprendimento, è finita?
Teorema di Convergenza del Perceptrone: se l'operazione
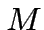 è linearmente separabile, allora la procedura di
apprendimento del Perceptrone converge, in un numero finito di
passi, ad una configurazione stazionaria in cui
è linearmente separabile, allora la procedura di
apprendimento del Perceptrone converge, in un numero finito di
passi, ad una configurazione stazionaria in cui
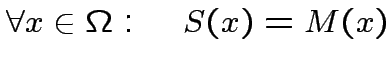 .
.
Dimostrazione:
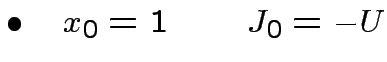
 Regola d'apprendimento:
Regola d'apprendimento:
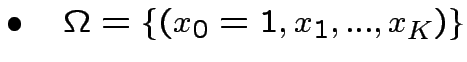 Passo 1. Separabiltà lineare:
Passo 1. Separabiltà lineare:
![$ M(x)=\theta[W\cdot x]$](img189.png) ,
, 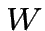 t.c.
t.c. 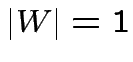
Passo 2. Disuguaglianze:
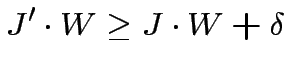 |
(1) |
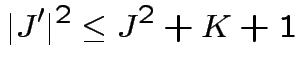 |
(2) |
Dopo 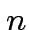 ripetizioni:
ripetizioni:
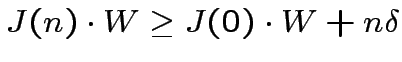 |
(3) |
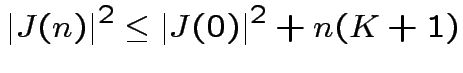 |
(4) |
Passo 3. Contraddizione:
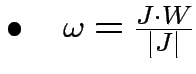
 Schwartz
Schwartz
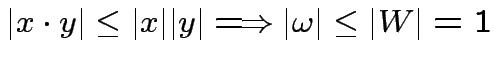
Dopo 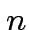 modifiche:
modifiche:
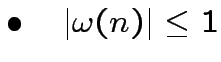 :
:
Poichè non possono più avvenire modifiche, il sistema deve essere
in una situazione stazionaria in cui
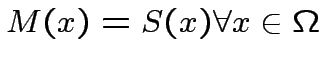 Dopo quanto converge la procedura di apprendimento?
Dopo quanto converge la procedura di apprendimento?
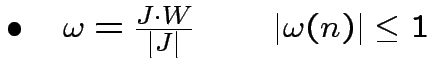
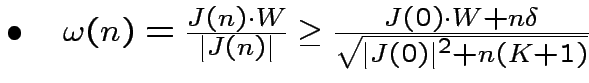
Se le condizioni iniziali sono
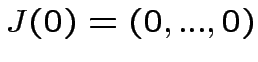 , otteniamo:
Osserviamo che
, otteniamo:
Osserviamo che 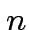 non è il numero di inputs, esempi da mostrare
al perceptrone, ma è il numero di modifiche: la procedura di
apprendimento può comunque essere molto lunga!
Versione "continua" del Perceptrone
non è il numero di inputs, esempi da mostrare
al perceptrone, ma è il numero di modifiche: la procedura di
apprendimento può comunque essere molto lunga!
Versione "continua" del Perceptrone
Procedura d'apprendimento:
Scelto a caso
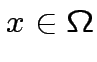 ,
,
![$ \Delta
J=\epsilon x[M(x)-\theta(J\cdot x)]$](img209.png)
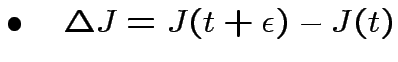
Si ottiene:
![$\displaystyle \frac{d}{dt}J(t)=\langle x[M(x_{l}-\theta(J(t)\cdot x)]\rangle_{\Omega}$](img211.png) |
(5) |
dove:
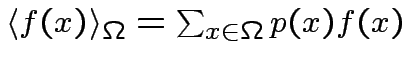
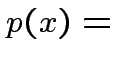 probabilità che il vettore
probabilità che il vettore 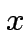 venga estratto durante il
processo di apprendimento.
venga estratto durante il
processo di apprendimento.
Teorema: Se il compito 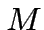 è linearmente separabile,
allora l'equazione (5) converge ad un punto
fisso
è linearmente separabile,
allora l'equazione (5) converge ad un punto
fisso 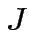 tale che
tale che
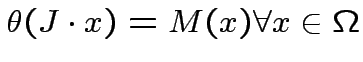 .
Come funziona l'apprendimento nelle "multilayer
feed-forward networks"?
.
Come funziona l'apprendimento nelle "multilayer
feed-forward networks"?
Data una rete con 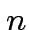 strati, abbiamo:
strati, abbiamo:
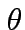 in questo caso si sceglie di tipo sigmoide.
in questo caso si sceglie di tipo sigmoide.
Dati
l'operazione 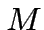 , al momento
, al momento 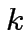 e l'input
e l'input 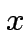 :
dove:
Kohonen's SOFM-model
:
dove:
Kohonen's SOFM-model
- Inizializzazione, vengono assegnati pesi random alle
sinapsi
- viene presentato un input
- Si trova la migliore unità e si caombiano i pesi
sinaptici
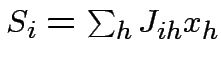
Dove:
 è un intorno del miglior neurone,
di raggio
è un intorno del miglior neurone,
di raggio
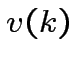 , al passo
, al passo 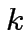 .
.
 è una funzione dipendente da dalla distanza tra
è una funzione dipendente da dalla distanza tra
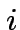 e
e 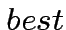 .
.



Next: About this document ...
Michele Cerulli
2000-10-29
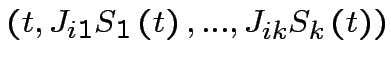 ;
;
![]() =
= ![]()
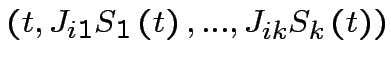 ;
;
![]() =
=
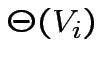 =
=
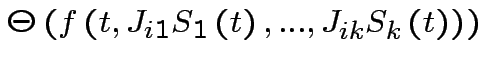 ;
;
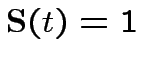 : il neurone al momento t è eccitato,
quindi produce un output;
: il neurone al momento t è eccitato,
quindi produce un output;
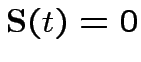 : il neurone al momento t non è eccitato,
quindi non produce alcun output;
: il neurone al momento t non è eccitato,
quindi non produce alcun output;
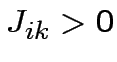 : la sinapsi che connette i due neuroni è
eccitativa, ovvero favorisce il passaggio di informazioni;
: la sinapsi che connette i due neuroni è
eccitativa, ovvero favorisce il passaggio di informazioni;
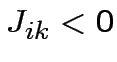 : la sinapsi è è inibitoria.
Il modello di McCulloch-Pitts
: la sinapsi è è inibitoria.
Il modello di McCulloch-Pitts
![$\displaystyle S_{i}(t+\Delta )=\theta \left[ \sum
^{N}_{k=1}J_{ik}S_{k}(t)-U_{i}\right] $](img12.png)
![\begin{displaymath}
\theta[x]=\{
\begin{array}{cc}
0 & x<0 \\
1 & x>0
\end{array}\end{displaymath}](img13.png)
![$\displaystyle \tau \frac{d}{dt}U_{i}\left( t\right) =\sum
^{N}_{k=1}J_{ik}g\left[ U_{k}(t-\tau _{ik})-U^{*}_{k}\right]+
$](img15.png)
![$\displaystyle -\rho U_{i}\left( t\right) \left\{ 1+\frac{\tau }{\Delta }\Theta
\left[ \int ^{\Delta }_{0}S_{i}(t-s)ds\right] \right\} $](img16.png)
![$\displaystyle g\left[ x\right] =\int ^{*}_{-\infty }P(u)du $](img17.png)
![$\displaystyle P(u)=Prob\left[ U_{i}(t)-U^{*}_{i}\in \left[ u,u+du\right]
\right]$](img18.png)
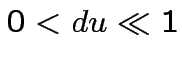 Graded Response Neurons. Si assume che la trasmissione
del messaggio avvenga istantaneamente,
Graded Response Neurons. Si assume che la trasmissione
del messaggio avvenga istantaneamente,
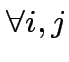 , e si trascurano i termini direset,
assumendo che le fluttuazioni del potenziale successive alla
trasmissione del messaggio siano irrilevanti:
, e si trascurano i termini direset,
assumendo che le fluttuazioni del potenziale successive alla
trasmissione del messaggio siano irrilevanti:
![$\displaystyle \tau \frac{d}{dt}U_{i}(t)=\sum ^{N}_{k=1}J_{ij}g\left[
U_{k}(t)-U^{*}_{k}\right] -\rho U_{i}(t) $](img22.png)
![$ g\left[ U-U^{*}\right] =\int ^{U-U^{*}}_{-\infty }P(u)du $](img23.png)
![$\displaystyle U_{i}(t)=f\left[ \phi
_{i}(t)\right] \qquad \qquad f\left[ \phi +2\pi \right] =f\left[
\phi \right]
$](img24.png)
![$\displaystyle \frac{d}{dt}\phi_{i}(t)=\omega_{i}+\sum^{N}_{k=1}J_{ik}\sin\left[\phi_{k}(t)-\phi_{i}(t)\right]
$](img25.png)
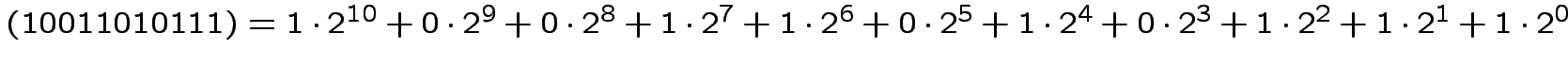 =1024+128+64+16+4+2+1=1239
=1024+128+64+16+4+2+1=1239
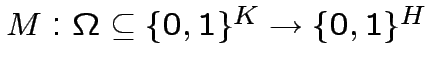
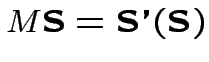
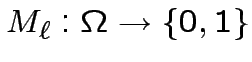
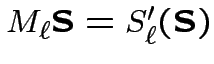
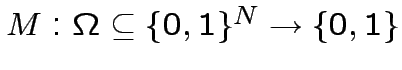 con i neuroni di
McCulloch-Pitts?
con i neuroni di
McCulloch-Pitts?
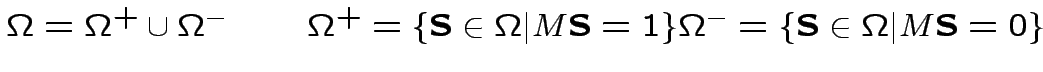
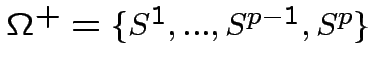
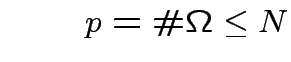
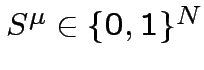
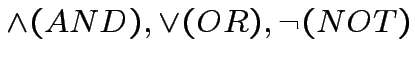 , definiamo
l'operatore
, definiamo
l'operatore 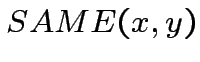 , che dice quando due variabili arbitrarie
hanno lo stesso valore:
, che dice quando due variabili arbitrarie
hanno lo stesso valore:
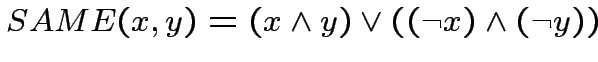
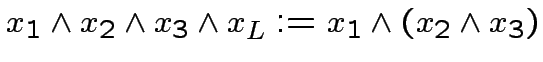
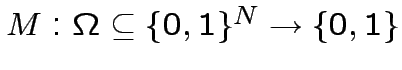 , una macchina
che la esegue può essere costruita, dati
, una macchina
che la esegue può essere costruita, dati
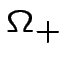 e il
vettore input
e il
vettore input
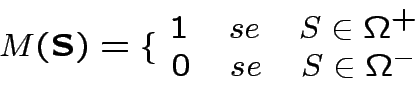
![]() ,
, ![]() e
e
![]() , si esprime:
, si esprime:
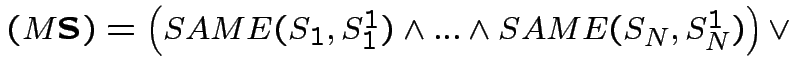
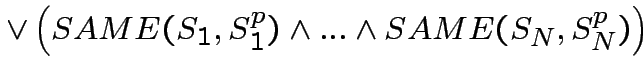
![$\displaystyle S_{i}(t+\Delta )=\theta \left[ \sum
^{N}_{k=1}J_{ik}S_{k}(t)-U_{i}\right] $](img12.png)
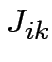 e
e 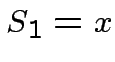 e
e
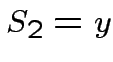 (
(
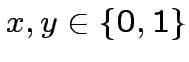 ).
).
![$\displaystyle S(t+\Delta )=\theta \left[ \sum
^{2}_{k=1}J_{k}S_{k}(t)-U^{*}\right]$](img57.png)
![$\displaystyle S(t+\Delta )= \theta \left[J_{1}x+J_{2}y-U^{*}\right]$](img58.png)

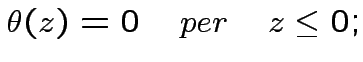
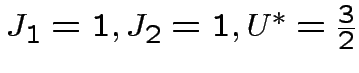
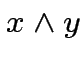
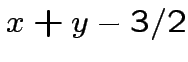
![$ \theta\left[x+y-3/2\right]$](img66.png)
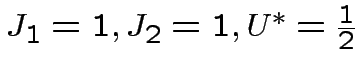
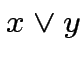
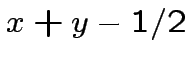
![$ \theta\left[x+y-1/2\right]$](img70.png)
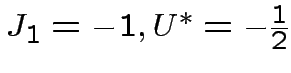
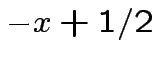
![$ \theta\left[-x+1/2\right]$](img74.png)
![$\displaystyle S_{i}(t+\Delta )=\theta \left[ \sum
^{N}_{k=1}J_{ik}S_{k}(t)-U_{i}\right] $](img12.png)
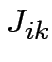 ed
ed
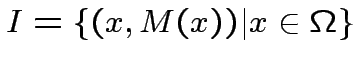
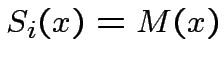 si
lascia tutto inalterato, altrimenti si modificano i parametri
caratterizzanti il neurone studente
si
lascia tutto inalterato, altrimenti si modificano i parametri
caratterizzanti il neurone studente 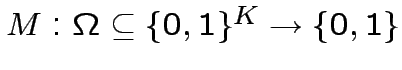
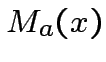
![$ \theta[-1]$](img81.png)
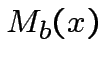
![$ \theta[-x+1/2]$](img83.png)
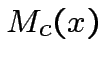
![$ \theta[x-1/2]$](img85.png)
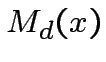
![$ \theta[1]$](img87.png)
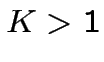 un solo neurone non basta, ad esempio, per eseguire
XOR(x,y):
un solo neurone non basta, ad esempio, per eseguire
XOR(x,y):
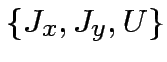 tali che:
tali che:
![$\displaystyle \theta\left[J_{x}x+J_{y}y-U\right]=XOR(x,y)\qquad\forall(x,y)\in\{0,1\}^{2}
$](img90.png)
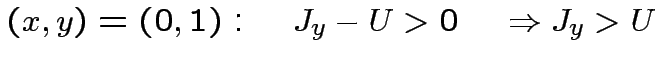
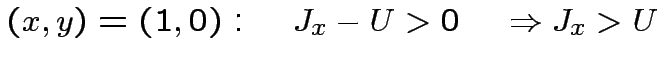
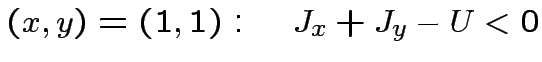
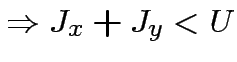
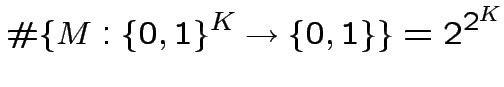
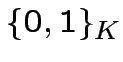 dei possibili vettori input corrisponde
ai vertici dell'ipercubo unitario in
dei possibili vettori input corrisponde
ai vertici dell'ipercubo unitario in ![]() , mentre il neurone
che esegue l'operazione
, mentre il neurone
che esegue l'operazione
![$\displaystyle S:\{0,1\}^{K}\rightarrow\{0,1\}\qquad
S(x)=\theta\left[\sum^{K}_{k=1}J_{k}x_{k}-U\right]$](img98.png)
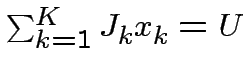
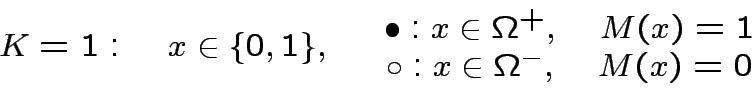

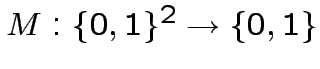 , 16 modi di colorare
i quattro vertici del quadrato:
, 16 modi di colorare
i quattro vertici del quadrato:
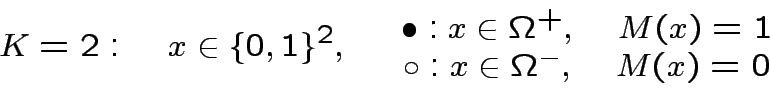
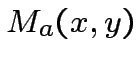
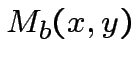
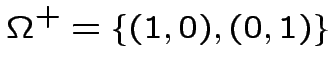

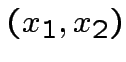
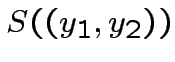
![$ y_{1}=\theta\left[W_{11}x_{1}+W_{21}x_{2}-V_{1}\right]$](img127.png)
![$ y_{2}=\left[W_{12}x_{1}+W_{22}x_{2}-V_{2}\right]$](img128.png)
![$ S((y_{1},y_{2}))=\theta\left[J_{1}y_{1}+J_{2}y_{2}-U\right]$](img129.png)
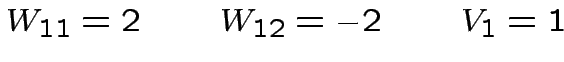
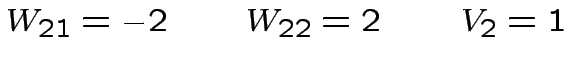
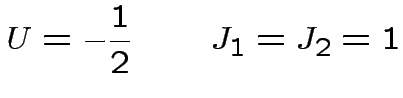
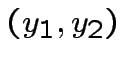

![$ \theta[2x_{1}-2x_{2}-1]$](img134.png)
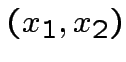
![$ \theta\left[y_{1}+y_{2}-1/2\right]$](img135.png)
![$ \theta[-2x_{1}+2x_{2}-1]$](img136.png)
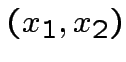
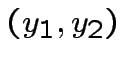
![$ \theta\left[y_{1}+y_{2}-1/2\right]$](img135.png)
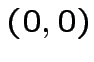
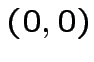
![$ \theta[0+0-1/2]=0$](img138.png)
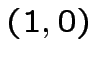
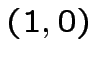
![$ \theta[1+0-1/2]=1$](img140.png)
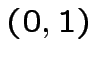
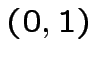
![$ \theta[0+1-1/2]=1$](img142.png)
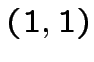
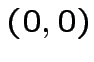
![$ \theta[0+0-1/2]=0$](img138.png)
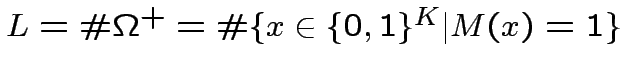

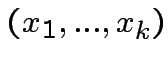
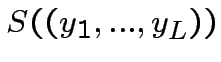
![$ y_{i}=\theta\left[\sum^{K}_{j=1}W_{ij}x_{j}-V\right]$](img148.png)
![$ S((y_{1},...,y_{L}))=\theta\left[\sum^{L}_{i=1}J_{i}y_{i}-U\right]$](img149.png)
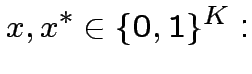
![$\displaystyle G\left[x^{*};x\right]=\theta\left[\sum^{K}_{i=1}(2x_{i}-1)(2x^{*}_{i}-1)-K+1\right]
$](img152.png)
![$ G\left[x^{*};x\right]=1\quad\Leftrightarrow\quad x=x^{*}$](img153.png)
![$ \bullet\quad G\left[x^{*};x\right]=1\quad\Leftarrow\quad
x=x^{*}$](img154.png)
![$\displaystyle G\left[x;x\right]=\theta\left[\sum^{K}_{i=1}(2x_{i}-1)^{2}-K+1\right]=$](img155.png)
![$\displaystyle =\theta\left[\sum^{K}_{i=1}1-K+1\right]=1
$](img156.png)
![$ \bullet\quad x\neq x^{*}\Rightarrow
G\left[x^{*};x\right]=0$](img157.png) :
:
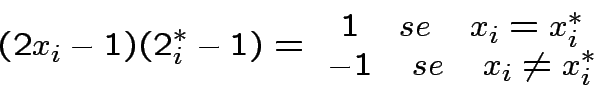
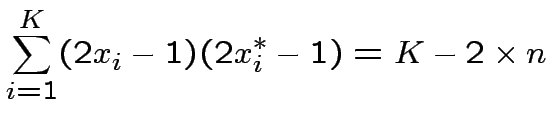
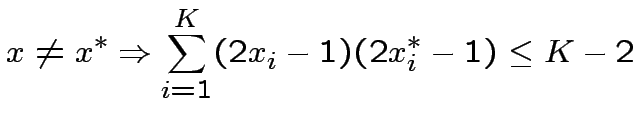
![$\displaystyle \Rightarrow G\left[x^{*};x\right]\leq \theta[K-2-K+1]=\theta[-1]=0
$](img161.png)
![$ G[x^{*};x]$](img163.png) , interpretata come
una operazione effettuata sulla variabile
, interpretata come
una operazione effettuata sulla variabile ![$\displaystyle G\left[x^{*};x\right]=\theta\left[2\sum^{K}_{i=1}(2x^{*}_{i}-1)x_{i}-2\sum^{K}_{i=1}x^{*}+1\right]
$](img164.png)
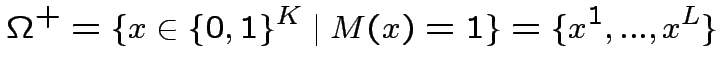
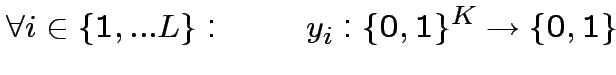
![$\displaystyle y_{i}=G\left[x^{*};x\right]=\theta\left[2\sum^{K}_{i=1}(2x^{*}_{i}-1)x_{i}-2\sum^{K}_{i=1}x^{*}+1\right]
$](img167.png)
![$\displaystyle y_{i}=\theta\left[\sum^{K}_{j=1}W_{ij}x_{j}-V\right] \qquad
S(y)=\theta\left[\sum^{L}_{i=1}y_{i}-\frac{1}{2}\right]
$](img168.png)
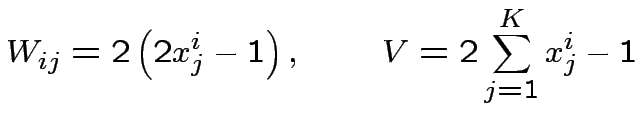
![$\displaystyle S(x)=\theta\left[\sum^{K}_{j=1}J_{ij}x_{j}-V\right]=\theta[J\cdot
x-U]
$](img170.png)
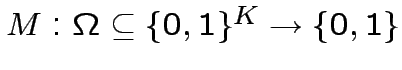
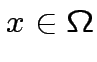 qualsiasi.
qualsiasi.
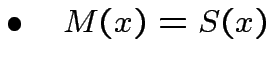 : torna al passo 1
: torna al passo 1
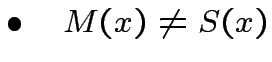 : modifica parametri e torna al passo 1
: modifica parametri e torna al passo 1
![$ J\quad\rightarrow\quad J+\Delta J[J,U;x,M(x)]$](img174.png)
![$ U\quad\rightarrow\quad U+\Delta U[J,U;x,M(x)]$](img175.png)
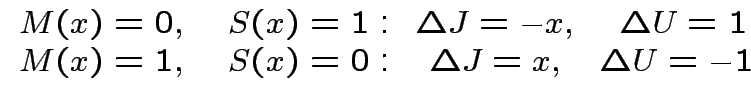
![$ J\quad\rightarrow\quad J+\Delta J[J,U;x,M(x)]$](img174.png)
![$ U\quad\rightarrow\quad U+\Delta U[J,U;x,M(x)]$](img175.png)
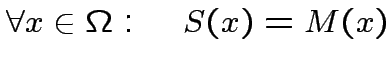 .
.
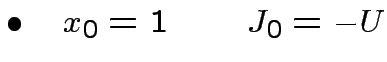
![$\displaystyle S(x)=\theta[J\cdot x],\quad
x=(x_{0},x_{1},...,x_{K})\in\{0,1\}^{K+1}
$](img180.png)
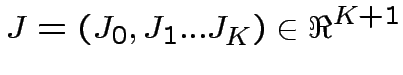
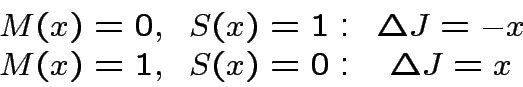
![$\displaystyle \Delta J=[2M(x)-1]x
$](img185.png)
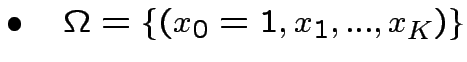 Passo 1. Separabiltà lineare:
Passo 1. Separabiltà lineare:
![$\displaystyle \exists W\in\Re^{K+1}\quad t.c.\quad\forall x\in \Omega:\quad M(x)=\theta[W\cdot x]$](img187.png)
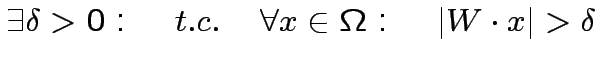
![$ M(x)=\theta[W\cdot x]$](img189.png) ,
, 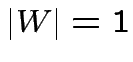
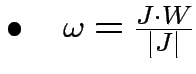
![]() Schwartz
Schwartz
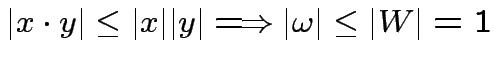
![]() modifiche:
modifiche:
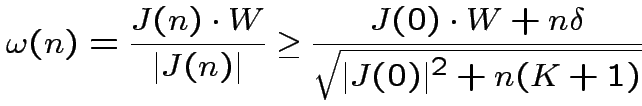
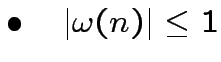 :
:
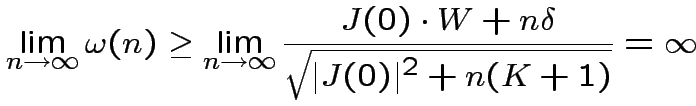
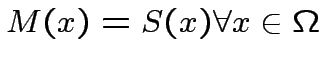 Dopo quanto converge la procedura di apprendimento?
Dopo quanto converge la procedura di apprendimento?
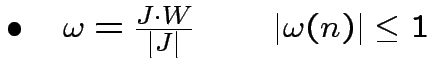
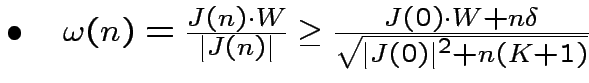
![$\displaystyle \frac{[J(0)\cdot W+n_{max}\delta]^{2}}{\vert J(0)^{2}+n_{max}(K+1)}=1
$](img205.png)
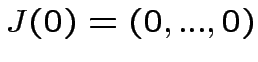 , otteniamo:
, otteniamo:
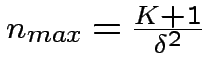
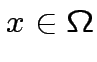 ,
,
![$ \Delta
J=\epsilon x[M(x)-\theta(J\cdot x)]$](img209.png)
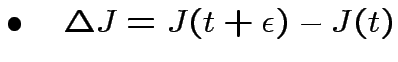
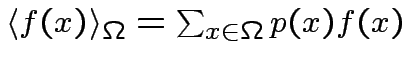
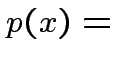 probabilità che il vettore
probabilità che il vettore 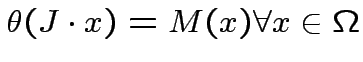 .
Come funziona l'apprendimento nelle "multilayer
feed-forward networks"?
.
Come funziona l'apprendimento nelle "multilayer
feed-forward networks"?
![$\displaystyle S^{l}_{i}=\theta[\sum_{h}J^{l}_{ih}]
$](img216.png)
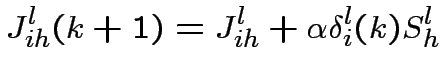
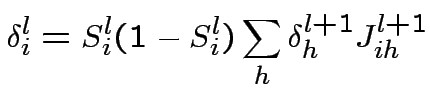
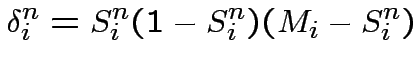
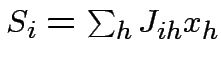
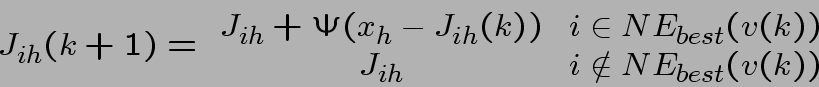
 è un intorno del miglior neurone,
di raggio
è un intorno del miglior neurone,
di raggio
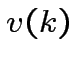 , al passo
, al passo